Существо проблемы вот в чём. Пусть есть функция

. Возьмём от неё полное приращение:

Теперь возьмём полное приращение второго порядка:

Теперь изменим ситуацию и параметризуем аргумент:
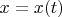
. Как известно, в таком случае

Это равенство эквивалентно

, если в него подставить
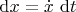
. Теперь попробуем написать второе равенство:
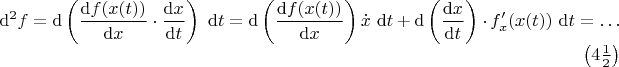
Здесь очевидно, что
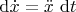
. Для того, чтобы найти
![$\mathrm d(f'_x[x(t)])$ $\mathrm d(f'_x[x(t)])$](https://dxdy-04.korotkov.co.uk/f/7/5/7/7570752f1ba7d2110f458592959e8d4582.png)
, используем правило о сложной функции:
![$\mathrm d(f'_x[x(t)]) = f''_{xx} \dot x \ \mathrm dt$ $\mathrm d(f'_x[x(t)]) = f''_{xx} \dot x \ \mathrm dt$](https://dxdy-03.korotkov.co.uk/f/a/4/c/a4cd4509f340d8f8d14618de41232db582.png)
. Постановка этих двух равенств в
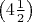
даёт окончательно равенство

:
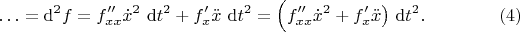
Легко видеть, что в среднюю часть

входит слагаемое вида
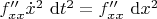
. Это то слагаемое, которое получается при подстановке
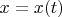
в

. Утверждение о "неинвариантности второго дифференциала" говорит о том, что так делать нельзя.
Однако, второе слагаемое имеет вид
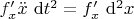
. Всю вместе формулу

можно формально переписать в виде

который получается и из других соображений:
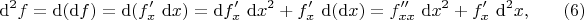
если положить, что в случае, когда

свободная переменная, то
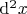
равен нулю, а если

сам является функцией, то
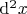
нулю уже не равен.
Так в чём состоит польза от утверждения, что второй дифференциал "не инвариантный"? Ведь если подставлять туда
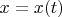
в его правильную форму
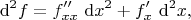
то всё становится на свои места.



