Как мне кажется, предложенное доказательство можно несколько упростить. Хотя идея, в сущности, та же самая.
При

справедливо равенство

.
Пусть

--- фиксировано. Тогда при

имеем

А значит

Как то с этими о маленькими и О большими все непонятно. Мудрено. Напишу то решение, которое задумал. Уверен, что Вы то же самое и имели ввиду.
Предположим, что

не стремится к нулю при

. Тогда существуют
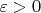
и строго возрастающая последовательность

такие, что

. Пусть для определённости

(при

всё аналогично). Так как

при

, то по теореме Лагранжа

при

. Геометрически это означает, что график функции при

лежит выше прямой, проходящей через точку

с угловым коэффициентом

. Эта прямая пересекает ось абсцисс в точке

. Следовательно

площади треугольника с основанием

и высотой

, т.е.

. Тогда

Так как

получаем противоречие с условием 2) стартового сообщения.
-- Вт фев 28, 2017 20:54:51 --по теореме Арцела–Асколи оно предкомпактно ...
Жуть! )))



