Пусть есть два твёрдых тела, положение которых в пространстве задаётся координатами центров масс и единичными кватернионами, задающими поворот ортонормированного базиса в неподвижной ИСО (будем называть её мировой системой координат и обозначим W) в базис, жёстко связанный с телом (так и будем называть его базис тела A / базис тела B; обозначать будем A'/B'). Так что если

-- координатный столбец вектора в W, то его координатный столбец в A' --

. Скорости пусть задаются координатами вектора скорости центра масс в W и координатами вектора угловой скорости в A'/B'. Я хочу ограничить относительное движение тел так, чтобы они могли свободно (и, для простоты, неограниченно) вращаться относительно общей оси.
(Как на картинке.)
Как выглядят правильные функции связей (функции, обращающиеся в ноль тогда и только тогда, когда координаты удовлетворяют связям (в идеале; на крайний случай -- в некоторой области корфигурационного пространства))? Сосредоточимся на связи, ограничивающей вращения, т.к. трансляционная тривиальна.
Если бы ось вращения была бы коллинеарна оси Z в A', то всё было бы просто: кватернион "относительной ориентации"

должен иметь мнимую часть только "вдоль третьей компоненты":

.
Но общий случай можно свести к нему, подправив

следующим образом:

, где

-- какой-нибудь кватернион, описывающий вращение вектора с координатами
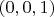
в

-- столбец с координатами единичного направляющего вектора оси вращения в системе координат A';

-- аналогично.

и

постоянны. Не ошибаюсь ли я где-нибудь?
Хочется связей именно такого вида -- непосредственно на кватернионы, а не что-то типа

для тела A и аналогично для B, где

-- неколлинеарные орты, нормальные к

, жёство связанные с телом A. С этим можно жить, но такой подход имеет недостатки. Во-первых, информация об ориентирующих кватернионах используется неявно, а во-вторых, такие уравнения связей выполнены и тогда, когда связь нарушена: если одно из тел повернуть на

градусов "в запретном направлении" (вокруг

, например):

. Что неприятно как само по себе, так и потому, что при численном решении уравнений (да, весь сыр-бор ради этого), лагранжевой системы со связями, сходимость в последнем (бистабильном) случае явно будет хуже, т.к. "возвращающая сила" (пропорциональная множителям Лагранжа), по идее, будет слабеть, при приближении системы к точке поворота на

градусов в запретном направлении, обращаясь в ноль при нём (такая прикидка: при повороте на

градус возвращающая сила в одну сторону вращает, при повороте на

-- в другую; непрерывная функция принимающая значения разных знаков на концах отрезка где-то зануляется -- где это делать, как не посередине).



