2. Локальная теория.
а)Для гладких функций

решение есть всегда
б) В аналитическом случае: решение можно искать в виде ряда с неопределенными к-тами. Система полученных уравнений всегда разрешима (если

). Но полученные ряды могут расходиться.
При

, ряды сходятся. При
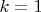
ряды, как правило, расходятся (нет аналитических решений). При этом: ни по какому конечному отрезку Тейлоровского разложения

в нуле вывод о том, есть решение или нет, сделать нельзя.
Для

, кажется, доказано отсутствие даже локальных решений
3. Есть и полулокальные задачи, типа : решить уравнение на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
для

. Вроде, об этом есть статья Экалля в Вестнике ЛГУ (№13, вып.3, 1973, 166-167)
4. Близкие задачи, подходы.
а) Задача о включении (отображения в поток): для данного

, найти

, такое, что

. Если бы мы сумели решить это уравнение, то в качестве Вашего решения

можно взять сдвиг за пдходящее время вдоль поля

б) Уравнение Абеля

. Заменой можно свести к а)
5. На этой (или родственных) задаче из классиков засветились: Абель, Фату, Адамар, Биркгоф. Обзор результатов по локальной задаче можно найти в одной из глав монографии M. Kuczma Functional equations in a single variables. Monogr. Matem., v
.46, Warsawa,1968
-- 27.02.2016, 20:51 --(я, собственно, оттуда и черпал в былые аспирантские годы инфу по истории вопроса).
sergei1961Ну, так, чтобы конкретно об этой задаче - по-моему, и нет нигде.
Из боле-мене современных - есть не очень давняя монография Жолондека (Zolodek H. "Monodromy" ? примерно так - нет под рукой ), в которой что-то про все это есть - в разделе о локальной классификации ростков одномерных диффеоморфизмов. А вообще, народ обычно что-то более общее ковыряет, а потом эту задачу смотрят как прикладную.
-- 27.02.2016, 20:53 --Ну да, именно так: статьи сурово специализированные, а про эту задачу - кусочек тут, кусочек там...



