Зарядка и разрядка конденсатора + теория цепей

[Krogg]

Здравствуйте, очень нужна помощь по данной теме и по решению подобных задач. Самого решения задачи у меня нет. Мне очень нужно разобраться и понять физику процесса на этом примере, чтоб решать такие задачи самому

Дана следующая схема:



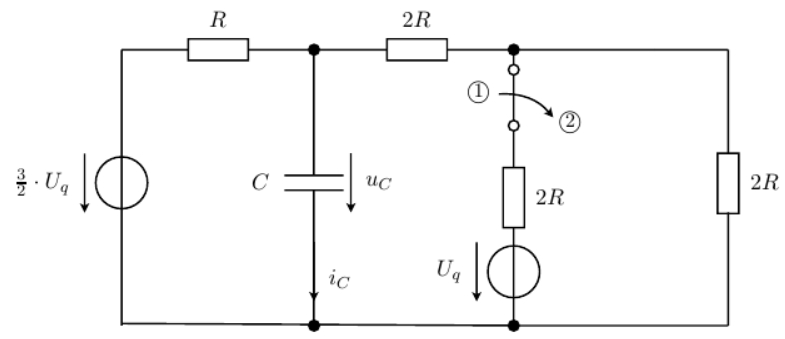
Данная схема находится в момент времени $t_1$ в стационарном состоянии. Ключ в позиции 1 замкнут
Даны следующие данные: $C = 2 mF, R = 1 k\Omega, U_q = 8 V$

a) Какова величина напряжения $U_c$ и тока $I_c$ на конденсаторе?

b) В монет $t_2$ ключ разомкнули. Каково напряжение $U_c$ $(t=t_2)$? Каково напряжение $U_c$ $(t\to \infty)$?

c) Вычислите постоянную времени $\tau$

d) Какова величина тока $I_c$ $(t<t_2)$? Каковa величина тока $I_c$ $(t\to \infty)$?

e) Нарисуйте график тока конденсатора в промежутке $t_1 \le t \le 5\tau$ и отметьте главные параметры на нем

f) Нарисуйте график напряжения конденсатора в промежутке $t_1 \le t \le 5\tau$ и отметьте главные параметры на нем

g) Задайте функцию напряжения $U_c (t \ge t_2) $

Возможно сами задания выглядят чуть коряво, но я думаю суть ясна

UPD:

Мои мысли по поводу решения задачи следующие:

Прочитал, что схему с одним конденсатором, сопротивлениями и источниками напряжения можно по теореме Тевенина заменить на следующую схему, при том для каждого положения ключа должна быть своя схема



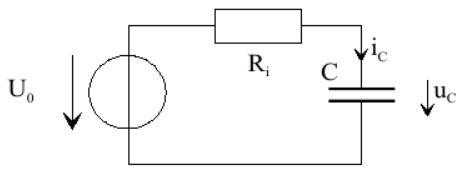
Где $R_i$ эквивалентное внутреннее сопротивление, а $U_0$ эквивалентное напряжение

Что бы найти их я убираю мысленно ветку с конденсатором, и вычисляю искомое сопротивление и напряжение исходя из этих двух клемм.

Если я исхожу из верхнего узла в ветке конденсатора, накоротко замыкаю источники напряжения, то $R_i = (R \parallel (2R + ( 2R \parallel 2R))) = 750\Omega$

С нахождением $U_0$, т.е. в данном случае с напряжением между клеммами в ветке конденсатора, оно же напряжение конденсатора у меня проблемы, меня смущает второй правый источник напряжения, поэтому у меня есть идея найти ток короткого замыкания $I_k$, а уже из него по формуле $U_0$ = $R_i$ $I_k$ найти искомое сопротивление

Возможно сопротивление $U_0$ можно найти проще и я обычно его всегда и нахожу без тока короткого замыкания, но в данной цепи для меня оно не очевидно, буду благодарен, если кто-то сходу увидит и подскажет чему оно равно

Верен ли в целом ход моих мыслей ?

$I_k$ я думаю находить по принципу суперпозиции, отключая по очереди источники напряжения находить ток в искомой ветке

Для левого источника напряжения получается такая схема:


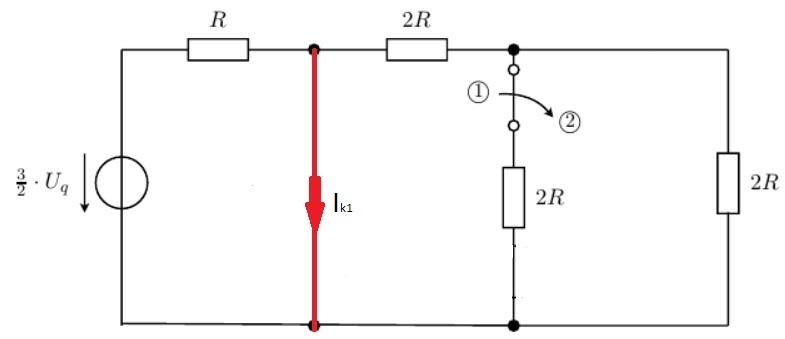
Откуда $I_{k_1} = \frac{12V}{1 k\Omega} = 0,012A$ = 12mA$

Для правого источника напряжения получается такая:


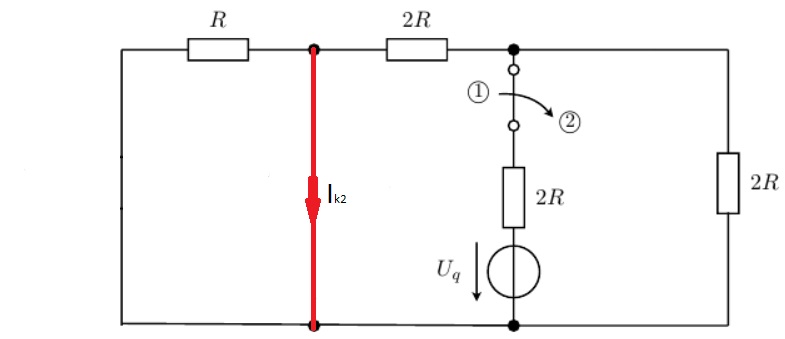
Нахожу сначала ток в ветке с источником напряжения: $I_q = \frac{U_q}{2R} = 4 mA$

Затем с помощью делителя тока нахожу ток в левой ветке: $I_{k_2} = I_q \frac{2R}{2R+2R} = 2 mA$

Суммирую оба тока, перемножаю с $R_i$ и нахожу искомое $U_0 = 10,5V$

Полная чушь или доля разума в этом есть? Может все же как-то $U_0$ можно сходу найти без вычисления тока

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задач.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»

[svv]

Krogg
Мне кажется, вместо подыскивания частных приёмов Вам надо применить общий метод — с помощью законов Кирхгофа составить систему уравнений для токов и напряжений. Должно получиться две системы — для замкнутого и разомкнутого положения ключа. Затем решить их относительно интересующих величин.

[Krogg]

svv
Если бы это был переменный ток, то я так и делал бы. Честно говоря ни разу не видел, чтоб задачи в цепях постоянного тока с конденсаторами решали через Кирхгофа.

Я нашел маленький пример от препода, где показывается решение именно методом эквивалентного генератора

В целом, если решать как я, то правильно ли я все нашел?

[svv]

Krogg в сообщении #1098522 писал(а):

Честно говоря ни разу не видел, чтоб задачи в цепях постоянного тока с конденсаторами решали через Кирхгофа.

Для конденсатора связь между током и напряжением такая: $I_C=C\frac{dU_C}{dt}$ (при согласованном выборе направлений). В стационарном состоянии $\frac{dU_C}{dt}=0$, отсюда $I_C=0$, а $U_C$ определяется другими элементами.

Krogg в сообщении #1098522 писал(а):

В целом, если решать как я, то правильно ли я все нашел?

Извините, не проверял.

[rustot]

Стационарное состояние - означает что ток через конденсатор прекратился. Поэтому начальное и конечное стационарные состояния вы можете найти просто заменив конденсатор на разрыв цепи. Останется найти эквивалентное внутреннее сопротивление источника чтобы рассчитать переходные процессы. Оно находится заменой конденсатора на перемычку и деление найденного ранее напряжения (когда заменяли конденсатор на разрыв цепи) на ток через эту перемычку. Задача сводится к тому что конденсатор заряженный до известного напряжения (первое стационарное состояние) подключается к источнику с известными эдс и внутренним сопротивлением

[AnatolyBa]

Krogg
Можно и так решать как вы.
Только здесь ошибка

Krogg в сообщении #1098347 писал(а):

Нахожу сначала ток в ветке с источником напряжения: $I_q = \frac{U_q}{2R} = 4 mA$

Нужно делить на $3R$
Можно не находить ток короткого замыкания, а сразу применить принцип суперпозиции для нахождения $U_0$
Можно преобразовать ЭДС в источник тока. Это иногда полезно, но пожалуй не в этом случае.
Можно для облегчения преобразовать две правые ветки в одну - по той же теореме Тевенина

[Krogg]

Спасибо всем за ответы, вы мне очень помогаете!

rustot в сообщении #1098532 писал(а):

Останется найти эквивалентное внутреннее сопротивление источника чтобы рассчитать переходные процессы.

Как раз таким образом я и начал решать, вы не могли бы глянуть правильно ли я его нашел?

rustot в сообщении #1098532 писал(а):

Оно находится заменой конденсатора на перемычку и деление найденного ранее напряжения (когда заменяли конденсатор на разрыв цепи) на ток через эту перемычку.

Дело в том, что у меня данная схема вызвала трудность при поиске этого напряжения (которое находится при замене конденсатора на разрыв цепи), поэтому я нашел ток, заменив конденсатор на перемычку, и умножил его на эквивалентное внутреннее сопротивление, таким образом выйдя на это напряжение. Вы не могли бы, пожалуйста, посмотреть правильно ли я нашел ток и это сопротивление

-- 10.02.2016, 23:51 --

AnatolyBa

AnatolyBa в сообщении #1098538 писал(а):

Нужно делить на $3R$

Не могу понять почему на $3R$ :( Закон Ома же в ветке, сопротивление равно 2R, или я что-то не вижу?
Upd: Ступил, пардон, вижу почему $3R$, надо делить на общее сопротивление, а не на сопротивление в ветке

AnatolyBa в сообщении #1098538 писал(а):

Можно не находить ток короткого замыкания, а сразу применить принцип суперпозиции для нахождения $U_0$

Да, обычно я всегда в задачах на теорему Тевенина находил $U_0$, но тут я не вижу как это просто сделать, по принципу суперпозиции умею находить только токи:( Поэтому такой вариант показался проще. Если бы вы показали как тут найти $U_0$ не через ток, я был бы безгранично благодарен

-- 11.02.2016, 00:30 --

AnatolyBa

Посмотрите, пожалуйста, дальше. Раз решение сверху для замкнутого ключа в общем верное, то проделываю теперь тоже самое для разомкнутого

Эквивалентное сопротивление в данном случае $R_i = (R \parallel (2R +2R)) = 1 k\Omega$

Нахожу ток
Для левого источника

Ток получается точно такой же, как и при замкнутом ключе $I_{k_{11}} = \frac{12V}{1 k\Omega} = 0,012A$ = 12mA$

Для правого же

Получается, что $I_{k_{22}} =0 ?$ Т.к. ток в ветке не течет, или все же как-то течет?

[AnatolyBa]

Krogg в сообщении #1098541 писал(а):

Эквивалентное сопротивление в данном случае $R_i = (R \parallel (2R +2R)) = 1 k\Omega$

Проверьте арифметику

Krogg в сообщении #1098541 писал(а):

Получается, что $I_{k_{22}} =0 ?$ Т.к. ток в ветке не течет, или все же как-то течет?

Да, не течет

А находить $U_0$ прямо из принципа суперпозиции не более сложно. чем ток. Возьмите случай разомкнутого ключа. Выкиньте красную перемычку в вашей первой схеме, тогда напряжение на ее месте будет $\frac{3}{2}U_q\frac{2R+2R}{2R+2R+R}$ Вторая схема дает ноль

[rustot]

Krogg в сообщении #1098541 писал(а):

Дело в том, что у меня данная схема вызвала трудность при поиске этого напряжения (которое находится при замене конденсатора на разрыв цепи), поэтому я нашел ток, заменив конденсатор на перемычку, и умножил его на эквивалентное внутреннее сопротивление, таким образом выйдя на это напряжение. Вы не могли бы, пожалуйста, посмотреть правильно ли я нашел ток и это сопротивление

Это нужно делать только для второго состояния, для разомкнутого ключа, а там просто источник напряжения слева и делитель из резисторов. То есть напряжение равно 4/5 от эдс левого источника

[AnatolyBa]

А вообще, чтобы не былонедоразумений, хочу заметить, что в реальной жизни надо действовать как писал svv (а в еще более реальной жизни применяются симуляторы). Но я понимаю почему вам дают такие задачи. Хотят развить понимание физических процессов, интуитивное качественное и полуколичественное видение.

[Krogg]

AnatolyBa в сообщении #1098557 писал(а):

Проверьте арифметику

Не то написал, там 800$\Omega$

AnatolyBa в сообщении #1098557 писал(а):

А находить $U_0$ прямо из принципа суперпозиции не более сложно. чем ток. Возьмите случай разомкнутого ключа. Выкиньте красную перемычку в вашей первой схеме, тогда напряжение на ее месте будет $\frac{3}{2}U_q\frac{2R+2R}{2R+2R+R}$ Вторая схема дает ноль

Спасибо большое, делитель напряжения же это. Для разомкнутого ключа я вижу как его применить

Для замкнутого случая и левого источника напряжения тоже вижу как: ${U_{01}} = \frac{3}{2} U_{q} \frac{ 2R +( 2R \parallel 2R) }{R+2R +( 2R \parallel 2R)}$

А для правого уже нет

-- 11.02.2016, 08:32 --

rustot в сообщении #1098565 писал(а):

Это нужно делать только для второго состояния, для разомкнутого ключа, а там просто источник напряжения слева и делитель из резисторов. То есть напряжение равно 4/5 от эдс левого источника

Для меня это все пока не очевидно, но я сейчас читаю информацию в интернете и пытаюсь разобраться

AnatolyBa в сообщении #1098567 писал(а):

А вообще, чтобы не былонедоразумений, хочу заметить, что в реальной жизни надо действовать как писал svv (а в еще более реальной жизни применяются симуляторы). Но я понимаю почему вам дают такие задачи. Хотят развить понимание физических процессов, интуитивное качественное и полуколичественное видение.

Все так, и я ничего не понимаю в этом физическом процессе, но сейчас читаю про это и напишу как я понял этот процесс. Самое сложное в этой задаче для меня впереди

[Krogg]

Значит что у меня уже есть, свел схему в эквивалентную по теореме Тевенина

В данном случае:

Ключ замкнут: $U_0 = 10V$, $R_i = 750\Omega$

Ключ разомкнут: $U_0 = 9,6V$, $R_i = 800\Omega$

Задание а) было найти $U_c$ и $I_c$, когда ключ замкнут.
Правильно ли я понимаю, что искомое напряжение $U_c$ является найденным напряжением $U_0 = 10V$, а $I_c =0$. Делаю выводы из того, что, когда конденсатор подсоединили к этому источнику он зарядился от него, а ток в это время падал и дошел до нуля. Т.е. в начальных условиях этой задачи конденсатор заряжен, а ток был не нулевой, но стал в итоге нулевой, рискну предположить, что это происходило как-то так

[AnatolyBa]

Krogg в сообщении #1098571 писал(а):

А для правого уже нет

Разберетесь, я в вас верю. Но давайте применим еще прием (чтобы задача решалась устно). Давайте заменим две правые ветки на одну эквивалентную с ЭДС и сопротивлением - с помощью того же Тевинена. Там ЭДС будет $U_q/2$ а сопротивление $R$ Видите это?


Да, все правильно для а)