О диофантовом уравнении к гипотезе Римана

[bax_id_ea]

Доброго всем времени суток.
В источнике знаний $=$ википедии сообщается, что гипотеза Римана о распределении нулей дзета-функции была сформулирована в 1859 году ($=$155 лет). Гипотеза Римана эквивалентна утверждению о том, что следующее диофантово уравнение не имеет решений в неотрицательных целых числах:

$$(elg^2+\alpha-(b-xy)q^2)^2+ (q-b^{5^{60}})^2+ (\lambda+q^4-1-\lambda b^5)^2+ (\theta+2z-b^5)^2+ (u+t\theta-l)^2+ (y+m\theta-e)^2+ (n-q^{16})^2+$$

$$+((g+eq^3+lq^5+(2(e-z\lambda)(1+xb^5+g)^4+\lambda b^5+\lambda b^5 q^4)q^4)(n^2-n)+ (q^3-bl+l+\theta\lambda q^3+(b^5-2)q^5)(n^2-1)-r)^2+$$

$$+(p-2w s^2 r^2 n^2)^2+ (p^2 k^2-k^2+1-\tau^2)^2+ (4(c-ksn^2)^2+\eta-k^2)^2+ (r+1+hp-h-k)^2+ (a-(wn^2+1)rsn^2)^2+$$

$$+(2r+1+\varphi-c)^2+ (bw+ca-2c+4\alpha\gamma-5\gamma-d)^2+ ((a^2-1)c^2+1-d^2)^2+ ((a^2-1)i^2c^4+1-f^2)^2+$$

$$+(((a+f^2(d^2-a))^2-1)(2r+1+jc)^2+1-(d+of)^2)^2+ (((z+u+y)^2+u)^2+y-K)^2 = 0$$

где $K$ - некоторый большой фиксированный целочисленный коэффициент (который, в принципе, можно указать в явном виде), а остальные буквы обозначают переменные.

Неужели никто из участников форума не пытался решить это длинное, но, в общем-то, несложное уравнение? Я оочень сильно удивился, когда понял, что уравнение быстро сводится в абсурдное равенство элементарными методами $=$ прямыми целочисленными вычислениями.
Ниже вариант решения. Спросить хочу, с элементарной логикой нигде не напутано?

Данное диафантово уравнение представляет собой сумму девятнадцати квадратов, которая равна нулю. Нуль в итоговой сумме можно получить только в том случае, если нулю равен каждый квадрат $(0^2=0)$ из девятнадцати. И потому из одного уравнения можно составить систему из девятнадцати уравнений, каждое из которых имеет нулевую сумму.
Поскольку, переменные должны быть неотрицательными целыми числами, то в случае невозможности такого значения, переменная получит значение нулевое. Иначе нуль в итого не получить. Нулевое значение переменная может получить и по результатам вычисления. Кроме того, все уравнения были пересортированы из исходника под задачу поиска решения.

$$ \begin{cases} p^2 k^2-k^2+1-\tau^2=0\\ r+1+hp-h-k=0\\ p-2w s^2 r^2 n^2=0\\ a-(wn^2+1)rsn^2=0\\ (a^2-1)c^2+1-d^2=0\\ 2r+1+\varphi-c=0\\ (a^2-1)i^2c^4+1-f^2=0\\ ((a+f^2(d^2-a))^2-1)(2r+1+jc)^2+1-(d+of)^2=0\\ 4(c-ksn^2)^2+\eta-k^2=0\\ n-q^{16}=0\\ q-b^{5^{60}}=0\\ \lambda+q^4-1-\lambda b^5=0\\ \theta+2z-b^5=0\\ (g+eq^3+lq^5+(2(e-z\lambda)(1+xb^5+g)^4+\lambda b^5+\lambda b^5 q^4)q^4)(n^2-n)+\\ +(q^3-bl+l+\theta\lambda q^3+(b^5-2)q^5)(n^2-1)-r=0\\ u+t\theta-l=0\\ y+m\theta-e=0\\ elg^2+\alpha-(b-xy)q^2=0\\ bw+ca-2c+4\alpha\gamma-5\gamma-d=0\\ ((z+u+y)^2+u)^2+y-K=0 \end{cases} $$

Пошаговый разбор, с последовательным присвоением:

$$p^2 k^2+1=\tau^2+k^2\eqno (1.1)$$

$$p^2+1/k^2=\tau^2/k^2+1\eqno (1.2)$$

При любом целом $k>1$ целочисленного решения не получить. Присваивается $k=1$

$$p^2+1=\tau^2+1\eqno (1.3)$$

и тогда $p=\tau$.

$$r+hp=h\eqno (2)$$

В целых неотрицательных числах $=$ без вариантов $r=0,\;p=1,\;h=h$.

$$p=2w s^2 r^2 n^2\eqno (3)$$

Однако. Оказывается, переменная $p$, к тому же является произведением от $r=0$. Так что, $p=0$ и $h=0$. Ну, и $\tau=0$ тоже.

$$a=(wn^2+1)rsn^2\eqno (4)$$

Без вариантов $a=0$, поскольку $r=0$.

$$(-1)c^2+1=d^2\eqno (5.1)$$

$$1=c^2+d^2\eqno (5.2)$$

Первая вилка в решении. Неопределённость вычислений. Решений может быть два: $c=0,\;d=1$ или $c=1,\;d=0$.

$$1+\varphi=c\eqno (6)$$

Если $c=0$, тогда $\varphi=-1$, то есть отрицательное число. Значит $c=1,\;\varphi=0$ и $d=0$. Неопределённость ликвидирована.

$$(-1)i^2+1=f^2\eqno (7)$$

Опять вилка. Два решения: $f=0$ при $i=1$; $f=1$ при $i=0$.

$$(-1)(1+j)^2+1=(of)^2\eqno (8)$$

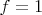
При любом $f$ уравнение принимает вид $-2j-j^2=(of)^2$, и потому $j$ может быть только нулём. Тогда $0=(of)^2$, и стало быть $j=0,\;f=0,\;i=1,\;o=o$.

$$4(1-sn^2)^2+\eta=1\eqno (9)$$

По условию $sn^2$ не может быть рациональным, а $\eta$ иметь отрицательное значение. Если $\eta=0$, то $(1-sn^2)^2=1/4$. Если $sn^2=0$ или $sn^2>1$, то $\eta<-2$.
И потому, без вариантов $\eta=1,\;sn^2=1$. Поскольку $sn^2=1$, то целочисленных значений, кроме $s=1$ и $n^2=1$, быть не может.
Wow=ваау. Оказывается $n=1$.

$$n=q^{16}\eqno (10)$$

$$q=b^{5^{60}}\eqno (11)$$

Получется, что и $q=1$ и $b=1$.

$$\lambda=\lambda\eqno (12)$$

$$\theta+2z=1\eqno (13)$$

По условию $z$ не может быть ни отрицательным, ни рациональным, так что $=$ без вариантов $\theta=1,\;z=0$.

$$(g+eq^3+lq^5+(2(e-z\lambda)(1+xb^5+g)^4+\lambda b^5+\lambda b^5 q^4)q^4)(n^2-n)+(q^3-bl+l+\theta\lambda q^3+(b^5-2)q^5)(n^2-1)=r\eqno (14.0)$$

Интересный момент. Именно с помощью этого уравнения задаются значения переменных $g,\;e,\;l,\;x$ и $\lambda$. Если выполнить все присвоения, то, поскольку $r=0$ и $n=1$, результатом будет пустое равенство $0=0$ с неустранимыми неопределённостями в дальнейших вычислениях. А потому, присваиваются все уже известные значения переменных, кроме $n$. И из одного уравнения получаются два уравнения с нулевой суммой:

$$(g+e+l+2e(1+x+g)^4+2\lambda)(n^2-n)=0\eqno (14.1.1)$$

$$g+e+l+2e(1+x+g)^4+2\lambda=0/(n^2-n)\eqno (14.1.2)$$

Без вариантов $g=0,\;e=0,\;l=0,\;x=x,\;\lambda=0$.

$$\lambda(n^2-1)=0\eqno (14.2.1)$$

$\lambda=0$ верно при любом $n$. Предыдущее вычисление подтверждено.

$$u+t=0\eqno (15)$$

Без вариантов $u=0,\;t=0$.

$$y+m=0\eqno (16)$$

Без вариантов $y=0,\;m=0$.

$$\alpha=1-xy\eqno (17)$$

Поскольку $xy=0$, то значение $x$ глубоко безразлично, а $\alpha=1$.

$$w=\gamma+2\eqno (18)$$

И да, значения $o,\;x$ и $w\geqslant2$ могут быть любыми. От них не зависит ничего. При вычислениях эти переменные умножаются на нуль.
Ну и, наконец, последнее уравнение:

$$((z+u+y)^2+u)^2+y-K=0\eqno (19)$$

Поскольку вычисленные значения всех переменных равны нулям: $z=0,\;u=0,\;y=0$, а $K$ по условию фиксированное целое число, то результат невозможно свести к нулевой сумме. Абсурдное равенство $0=K$.

И, да. Как отдельное уравнение $((z+u+y)^2+u)^2+y-K=0$ без проблем сводится к нулю в любых целых неотрицательных числах. В составе данного диофантова уравнения или в соответствущей ему системе уравнений $=$ решения нет ($=$ система несовместна).
Итого $=$ Данное диофантово уравнение не имеет решений в неотрицательных целых числах, поскольку при соблюдении этого условия представляет собой абсурдное равенство $K^2=0$, так как $K$ - некоторый большой фиксированный целочисленный коэффициент.

(baxea ps) Дополнительное пояснение. Первое уравнение имеет целочисленное решение, только если одна трёх переменных равна единице. Но если единице равны $p$ или $\tau$, то одна из переменных в уравнении (3) должна быть рациональным числом. Всё остальное $=$ бинарная логика.

[nnosipov]

bax_id_ea в сообщении #954772 писал(а):

Пошаговый разбор, с последовательным присвоением:

$$p^2 k^2+1=\tau^2+k^2\eqno (1.1)$$

$$p^2+1/k^2=\tau^2/k^2+1\eqno (1.2)$$

При любом целом $k>1$ целочисленного решения не получить.

Попробуйте взять $(p,k,\tau)=(2, 4, 7)$.

-- Ср дек 31, 2014 15:19:20 --

bax_id_ea в сообщении #954772 писал(а):

Дополнительное пояснение. Первое уравнение имеет целочисленное решение, только если одна трёх переменных равна единице.

Прежде чем что-то заявить, нужно подумать, есть ли этому заявлению хоть какое-то обоснование.

[12d3]

bax_id_ea в сообщении #954772 писал(а):

При любом целом $k>1$ целочисленного решения не получить.

Ошибка в самом начале. $p=8,\,\,k=16,\,\,t=127$ - решение. И таких решений, где $k>1$ - очень много.

[Tot]

bax_id_ea, topic87534.html
в качестве моей попытки.
Результаты моих попыток разобраться следующие.
1. Это универсальное диофантово уравнение, универсальный полином Джонса (иногда пишут Джоунса). Оно подходит для любой алгоритмической задачи. Коэффициент $K$ свой для каждого алгоритма. Существует теоретический метод его подсчёта. Можно прочитать в книге Матиясевича. Только на практике это чрезвычайно сложно.
2. Если желаете подоказывать гипотезу Римана, то лучше взять в той же книге систему из 6 уравнений, решение которой опровергает гипотезу, подставить туда систему диофантовых уравнений для степенной функции и работать с ней. Там правда один параметр будет под ограниченным квантором общности. Способ избавления от него в книге расписан весьма поверхностно, без деталей.
3. Если есть интерес к упрощению выписанного Вами полинома ради спортивного интереса, то что-то там есть, на мой взгляд. Хотя в одной из старых статей Матиясевича написано что-то вроде того, что эта задача сложнее многих других. Я потерял к уравнению интерес раньше, чем выписал объяснение того, как получил частное решение в той теме. Я рассматривал три варианта $b=0$; $b=1$; $b>1, q$- очень большое число.
Первое уравнение в Вашей системе расписываем уравнением Пелля. Затем множество решений анализируем вместе с вторым уравнением и так далее. Порядок уравнений для анализа у Вас правильный. Там где-то противоречие возникает, а где-то более простая система. Просто всё это представляет интерес лишь для профессиональных математиков. До практики на этом не доберёшься.
4. В скобке с коэффициентом $K$ кое-где вместо плюсов стоят в оригинальной статье знаки умножения, помещавший это в Википедию человек слегка попутал знаки.

[Rob123]

Данное диофантово уравнение НЕ представляет собой сумму девятнадцати квадратов (три из них не квадраты, одно со знаком -) . Легко ошибиться при таком количестве переменных. Однако поскольку сумма квадратов неотрицательна можно получить некоторое ограничение на эти четыре "нехороших" одночлена и только.