I said that with such unusual definition of

your formula of kinetic energy
is correct.
But such definition is source of potential mistakes and let me use everywhere below
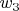
and
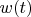
for angular speed of ring clockwise
in inertial reference frame. You can at any moment replace it back to your definitions via
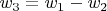
Friction

for first and last ring compensated by horizontal external forces

, that in sum consume power
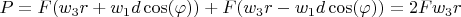
. For another intermediate rings it not competsated and each of them lose angular speed due sum of 2 friction forces.
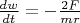
,
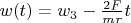
. With fixed

it will continues lineary till
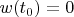
. From this moment there different behaviour for even and odd number of rings, but till this moment no difference and lets stop calculation at this moment
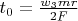
Heating power at each contact between ring

and ring

is
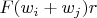
. Between intermediate rings (ie in
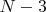
contact points) it
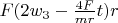
, and in 2 rest points it
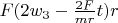
and in sum
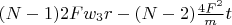
. And total heating energy during

is
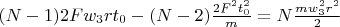
So during

on the one hand external 2 forces

did work
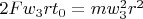
, intermediate rings lose
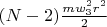
of kinetic energy, on the other hand we got
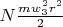
of heating energy. Balance is zero
As you can see,

finally do not affect anything. It affect for example work of upper external

but affect work of lower external

in opposite direction and as result do not affect summary external work. Only with strange definition of

it can appear in final result



