Попробую написать, что я пока понял. (
Не всё из этого может быть
верно, поэтому очень прошу поправить, если что не так!)
Изначально у нас имеется 2 абонента

и

, которые хотят
синхронизироваться. Для этого они случайным образом выбирают свои весовые коэффициенты (вектора), которые служат начальными условиями:

Далее, на каждом этапе ГСЧ генерирует случайные вектора:

После этого каждый пользователь считает величину:

где

и передаёт её напарнику. Далее возможны 2 варианта:
1. Если

, то веса не изменяются и процедура повторяется заново.
2. Если

, то каждый пользователь обновляет свои весовые коэффициенты согласно одному из (заранее оговоренных) правил:



где

Про функцию

и параметр

далее ничего не сказано. В другом источнике сказано, что

это step function. Погуглив, я предположил, что это то, что мы называем "простой функцией".
Объясните, пожалуйста, как она определяется в данном случае.Данная процедура продолжается до тех пор, пока не будет выполнено равенство:

Следующий вопрос:
как определить предыдущее равенство было достигнуто?Заранее большое спасибо за ответы
(Оффтоп)
Надоело самому с собой общаться

Можно переписать всё в виде матриц:

где
 -- Пт янв 18, 2013 15:23:33 --
-- Пт янв 18, 2013 15:23:33 --Также в данной статье написано, что:
Цитата:
During synchronization process, only the input vectors
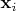
and the total outputs

are transmitted over the public channel.
Я не понимаю, зачем передавать вектора
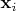
? Разве

не достаточно?
-- Пт янв 18, 2013 15:43:16 --Кажется, разобрался:

, а случайные вектора
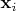
генерируется общий для двух участников и

для

,

для

.



