Вы таки прочитайте выше, я потом уточняла:
Вот у Вас там стоит слагаемое вида
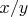
- оно о малое от чего?
Даже не так. Вы в Ваше разложение не вписали, в частности, слагаемое

, а оно там, в принципе, есть. Что, оно тоже войдет в

?
Хорошо бы если бы было так, но, к сожалению, мне надо сдавать контрольную работу, в которой этот самый номер...
Если бы мне в контрольной попалось такое задание,
Дана функция

,

. Мне нужно ее разложить до 2-го порядка в окрестности точки М.
(по формуле Маклорена), я бы написала, почему это сделать невозможно с полным обоснованием. Это было бы абсолютно верным и полным решением.
Если Вы считаете необходимым, тем не менее, непременно делать то, что Вам предлагают, - хотя нужды в этом нет, - Вы можете попробовать так, как предлагалось, и даже записать Вашу функцию в виде

, но число слагаемых в

будет бесконечным.
Повторюсь, умножьте на

(с тем, чтобы потом разделить), или делайте так, как Вам предложено, сразу вынеся

, числитель не трогайте, остальное разложите по

, скажем, до второй степени, получится сумма по

c к-тами, зависящими от

, а вот после этого раскладывайте эти коэффициенты. Где-то разложение будет содержать бесконечное число слагаемых, где-то оставьте только те, чтобы полученное было

.
Разложением до второго порядка это назвать все равно будет проблематично, поскольку в обычном тейлоровском разложении до

-го порядка присутствуют все порядки, начиная с первого и заканчивая

-м, по возрастанию. А какой порядок имеет, например, все тот же
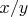
?
(Оффтоп)
Мое мнение по поводу задания осталось прежним.