n-ая производная имеет n-1 корень (Зорич V.3.6c)

[Urnwestek]

Пусть:
1) $f \in C^{(n)}(-1,1)$
2) $\sup\limits_{-1<x<1}|f(x)| \leqslant 1$
Тогда:
Существует такое число $\alpha_n$ зависящее только от $n$, что если $|f'(0)|>\alpha_n$, то уравнение $f^{(n)}(x) = 0$ имеет по крайней мере $n-1$ корень.

Задача: доказать это.

Будем считать доказанным следующие факты:
1)Пусть $m_k(I) = \inf\limits_{x \in I} |f^{(k)}(x)|$, где $I$ — промежуток содержащийся в $(-1,1)$
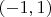
Пусть $I$ разбили на три последовательных промежутка $I_1,I_2,I_3$ и $\mu$ длина $I_2$, тогда выполняется:
$m_k(I) \leqslant \frac{1}{\mu}(m_{k-1}(I_1) + m_{k-1}(I_3))$
2) если $I$ имеет длину $\lambda$, то:
$m_k(I) \leqslant \frac{2^{k(k+1)/2}k^k}{\lambda^k}$

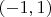
Зорич даёт указание: используйте факт 1) и по индукции докажите, что существует такая последовательность $x_{k_1},...,x_{k_k}$ интервала $(-1,1)$ что $f^{(k)}(x_{k_{i}}) \cdot f^{(k)}(x_{k_{i+1}}) < 0$

Я смог доказать лишь базу индукции, при $n=2$ доказательство:
1)Предположим, что функция $f^{(2)}$ не имеет нулей при любом $\alpha_2$, для определённости предположим, что $f^{(2)}(x)>0$, т.е. функция $f$ — выпуклая.
2)По свойствам выпуклых функций, $f$ сперва убывает на интервале $(-1,a)$ а затем возрастает на интервале $(a,1)$, где a — это такая точка, что $f'(a)=0$. Для определённости предположим, что $0 \in (a,1)$. Ограничим функцию $f$ до интервала $(a,1)$. Т.е. теперь функция $f$ — возрастающая.
3) Пусть $h>0$. По теореме Лагранжа $ f(h) = f(0)+ hf'(\zeta) \geqslant f(0) + hf'(0) $ (неравенство следует из выпуклости, т.е. возрастания производной).
4) Выберем $\alpha_2 = 10 < f'(0) = |f'(0)|$ вспомним, что $-1 \leqslant f(0) \leqslant 1$ и окончательно получим $f(h) \geqslant f(0) + hf'(0) \geqslant -1 + 10h $
5) Из неравенства выше следует, что $f(0.5) \geqslant -1 + 10\cdot0.5 > 1$ но это протеворечит тому, что $\sup\limits_{a<x<1}|f(x)| \leqslant 1$.
Полученное противоречие завершает доказательство.

Но как проталкивать индукцию и использовать то неравенство, на которое указывает Зорич, ума не приложу; если кто-то даст какие-то наводящие соображения — буду благодарен.

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Олимпиадные задачи (М)»
Причина переноса: перенёс с согласия автора в более подходящий раздел