Предрамсеевские графы для 
Известно точное значение


так что, если

.
Лемма 2.4. Если  , тогда
, тогда

Из Леммы 2.1 имеем

Также, из Формулы 1.15 получаем

то есть
 Лемма 2.5. Если
Лемма 2.5. Если  , тогда
, тогда 
 -связен и
-связен и  -связен.
-связен.Из Леммы 2.4 и Леммы 1.1 следует, что


-связен. Предположим, что

не

-связен. Тогда можно выделить две компоненты

и

без красных ребер между ними. Так как для каждой вершины

, то количество вершин в каждой компоненте больше

. Так как каждая компонента не содержит красных треугольников, то количество вершин в каждой компоненте больше

. Так как

, то

. В результате получаем, что

. Очевидно, что такой граф содержит

(см. рис. 2). Противоречие. Граф

-связен.

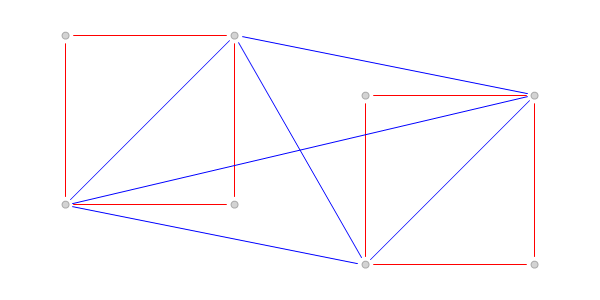 Рис. 2.
Рис. 2. 
.
Лемма 2.6. Если  , тогда
, тогда  . То есть, в графе найдется вершина с красной степенью, равной
. То есть, в графе найдется вершина с красной степенью, равной  .
.Допустим, что в графе нет вершины с красной степенью, равной

. Тогда, из Леммы 2.4 следует, что красные степени всех вершин равны

. Но тогда из

-связности графа следует, что

, в котором точно найдется

в качестве подграфа (см. рис. 3). Противоречие.

 Рис. 3.
Рис. 3. Случай, когда красные степени всех вершин равны

.
Лемма 2.7. Если  , тогда
, тогда  . То есть, в графе найдутся две вершины, соединенные красным ребром, красные степени которых равны
. То есть, в графе найдутся две вершины, соединенные красным ребром, красные степени которых равны  .
.Допустим, утверждение леммы ложно. По Лемме 2.6 найдется вершина

с красной степенью, равной

. Рассмотрим эту вершину. По предположению леммы, все соседи данной вершины имеют красные степени, равные

. Так как в графе нет красных треугольников, то никакие два из этих соседей не соединены красным ребром. Кроме вершины

каждая соседняя с ней вершина соединена красным ребром только с одной вершиной. То есть, в графе

найдется по крайней мере

вершина, не соединенная красным ребром ни с одним из соседей

. Таким образом в графе нашелся подграф

, вершинами которого являеются соседи вершины

и одна из вершин, не соединенная ни с одной из них красным ребром (см. рис. 4).

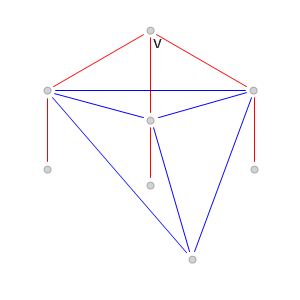 Рис. 4.
Рис. 4. Случай, когда нет двух вершин с красной степенью

, соединенных красным ребром.
Лемма 2.8. Если  , тогда в нем найдется красный цикл
, тогда в нем найдется красный цикл  , в котором две соседние вершины имеют красную степень, равную
, в котором две соседние вершины имеют красную степень, равную 
Рассмотрим произвольный граф

. Рассмотрим две его вершины с красной степенью, равной

, соединенные красным ребром (такие найдутся по Лемме 2.7). Пусть это вершины

и

. Кроме друг друга каждая из этих вершин соединена красными ребрами еще с двумя вершинами графа

. Пусть

. Ввиду отсутствия в графе

красных треугольников все вершины

различны. Так как вершины

не образуют

, то среди них найдутся две, соединенные красным ребром. То есть в графе

найдется красный цикл

в котором две соседние вершины имеют красную степень

(см. рис. 5).

 Рис. 5.
Рис. 5. Красный цикл

, в котором две соседние вершины имеют красную степень

.
Лемма 2.9. Если  , тогда в нем найдется красный цикл
, тогда в нем найдется красный цикл  , в котором две противоположные вершины имеют красную степень, равную
, в котором две противоположные вершины имеют красную степень, равную  .
.Предположим, утверждение леммы ложно. Рассмотрим красный цикл

, в котором две соседние вершины имеют красную степень, равную

(такая конструкция найдется по Лемме 2.8). Вершины рассматриваемой части графа обозначим

, при этом

образуют цикл,

(обозначения приведены на рис. 6).
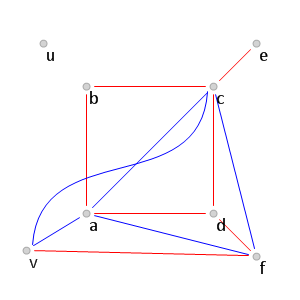 Рис. 6.
Рис. 6. Поиск красных ребер среди соединяющих вершины

.
Рассмотрим вершины

, они не образуют

. Так как граф

не содержит красных треугольников, и

, то среди ребер, соединяющих данные вершины, красными могут быть только

или

. По предположению леммы

, то есть

(см. рис. 6).
Аналогично, рассматривая вершины

, получим

. Далее, рассматривая вместо вершины

вершину

, получим

. Таким образом, имеем красный цикл, образованный вершинами

, причем

(см. рис. 7). Противоречие.

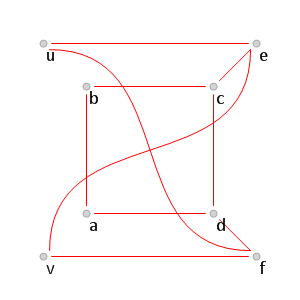 Рис. 7.
Рис. 7. Поиск красного цикла, в котором две противоположные вершины имеют степень, равную

.
Лемма 2.10. Если  , он содержит
, он содержит  в качестве подграфа.
в качестве подграфа.Рассмотрим красный цикл

в котором две противоположные вершины имеют степень, равную

(такая конструкция найдется по Лемме 2.9). Обозначим вершины, образующие цикл,

, пусть

. Обозначим вершины, смежные с вершинами

и

по красным ребрам и не принадлежащие красному циклу

через

и

соответственно. Так как вершины

не образуют

и

не содержит красных треугольников, то

(см. рис. 8).
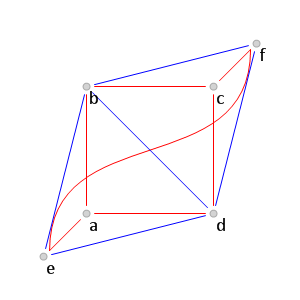 Рис. 8.
Рис. 8. Поиск красных ребер среди соединяющих вершины

.
Далее рассмотрим вершины

, не отображенные на рис. 8}. Рассмотрим вершины

. Так как они не образуют

, то хотя бы две из них соединены красным ребром. Так как

не содержит красных треугольников, то

. Следовательно, хотя бы одно одно из ребер

красное (см. рис. 9).
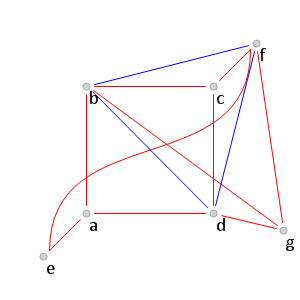 Рис. 9.
Рис. 9. Поиск красных ребер среди соединяющих вершины

.
Рассуждая аналогично, можно заключить что хотя бы одно из ребер

красное. Если предположить, что

, то получим

, то есть будет иметь красный треугольник

. Следовательно, хотя бы одно из ребер

красное. Без ограничения общности, будем считать, что

.
Теперь рассмотрим вместо вершины

вершину

. Для нее проведем аналогичные рассуждения, и получим, что хотя бы одно из ребер

должно быть красным. Однако

, то есть других красных ребер из вершины

выходить не может. Таким образом,

.
Аналогично цвету ребра

получим, что

(см. рис. 10). Нетрудно видеть, что в нашем графе последовательность вершин

образует красный цикл длины

.

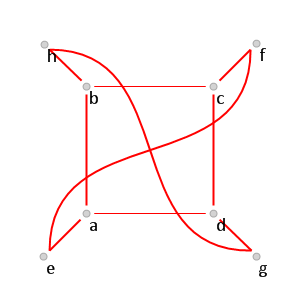 Рис. 10.
Рис. 10. Красный цикл

в графе

.
Теорема 2.2. 
Рассмотрим произвольный граф

. По Лемме 2.10 он содержит красный цикл длины

. Обозначим вершины, образующие цикл через

в порядке обхода цикла. Так как вершины

не образуют

, и граф не содержит красных треугольников, то одно из ребер

должно быть красным. Без ограничения общности, считаем, что

. Аналогично, рассматривая вершины

, получим, что

(см. рис. 11).
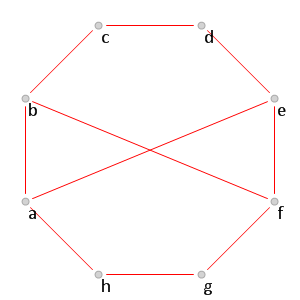 Рис. 11.
Рис. 11. Красная часть графа

, для которого

Полученный граф не содержит ни

, ни

, то есть является предрамсеевским графом, для которого

. Так как все построения выполнялись без ограничения общности, то полученный граф является единственным (с точностью до изоморфизма) предрамсеевским графом c

для числа Рамсея

.
Для получения предрамсеевского графа с

нужно покрасить в красный цвет одно из ребер, окрашивание которого не приведет к возникновению красного треугольника. Всего таких ребер

:

, - то есть, производя окраску каждого из этих ребер, мы получим

предрамсеевских графа с

. Все эти

графа попарно изоморфны.
Без ограничения общности будем считать, что для предрамсеевского графа, для которого выполняется

,

(см. рис. 12}).
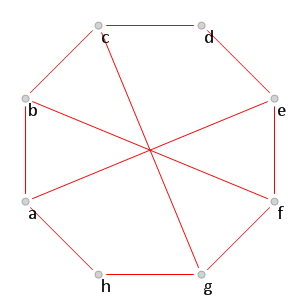 Рис. 12.
Рис. 12. Красная часть графа

, для которого

.
Для получения предрамсеевского графа с

нужно покрасить в красный цвет единственное ребро, окрашивание которого не приведет к возникновению красного треугольника. Это ребро

(см. рис. 13).
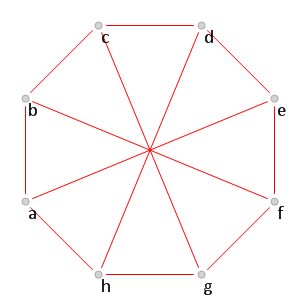 Рис. 13.
Рис. 13. Красная часть графа

, для которого

.
Таким образом, по построению без ограничения общности мы получили

попарно неизоморфных предрамсеевских графа для числа Рамсея

.

\\
Заметим, что для графа

верно следующее:



Отдельно отметим граф

, для которого значение

максимально (

). Его красный и синий подграфы являются циркулярными графами (см. рис. 14}):

 Рис. 14.
Рис. 14. Все ребра графа

, с максимальным значением

.



