Уравнение Эйлера

[EvilPhysicist]

Не могу понять, откуда в уравнении Эйлера $ \cfrac{\partial \vec v}{\partial t} +(\vec v \cdot \nabla) \vec v +\cfrac{1}{\rho} \nabla p $ член $(\vec v \cdot \nabla) \vec v$

Если брать вывод из уравнений Ньютона то понятно
1)$\cfrac{d}{dt} \vec p - \vec F=0 $
2)$ \int dV \left( \cfrac{d}{dt} \vec j + \nabla p \right)=0 $
И вот тут становится не понятно, как $ \cfrac{d}{dt}\vec j = \rho \left( \cfrac{\partial \vec v}{\partial t} +(\vec v \cdot \nabla) \vec v \right) $

Если брать формализм Эйлера, то можно выбрать систему координат, которая "ползёт" за веществом и в ней мы вроде как можем не беспокоится за то, что в выбранный нами объём попадёт лишний импульс и в ней должно быть $ \vec p = \int dV \vec j $ и соответственно уравнения Ньютона примут вид $\int dV \left( \cfrac{\partial \rho}{\partial t} \vec v + \rho \vec v + \nabla p \right)=0 $, что не очень похоже на уравнения Эйлера.

Если же брать формализм Лагранжа, то надо как-то среда ещё и течёт и выбранный объём попадает ещё импульс, что я вообще не понимаю как сделать.

Так вот, откуда берётся член $(\vec v \cdot \nabla) \vec v$ и в какой литературе подробно математически рассмотрен Лагранжев и Эйлеров формализм?

[В. Войтик]

EvilPhysicist в сообщении #613584 писал(а):

И вот тут становится не понятно, как $ \cfrac{d}{dt}\vec j = \rho \left( \cfrac{\partial \vec v}{\partial t} +(\vec v \cdot \nabla) \vec v \right) $

Насколько я понимаю $ \mathbf{j} = \rho \mathbf{v} $
$\frac{d\rho }{dt}=0$
$\frac{d\mathbf{v}}{dt}=\frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v}\nabla )\mathbf{v}$
Отсюда следует Ваше уравнение.

[Someone]

Формула полной производной:

$$\frac{d\vec v}{dt}=\frac{\partial\vec v}{\partial t}+\frac{\partial\vec v}{\partial x}\frac{dx}{dt}+\frac{\partial\vec v}{\partial y}\frac{dy}{dt}+\frac{\partial\vec v}{\partial z}\frac{dz}{dt}=$$

$$=\frac{\partial\vec v}{\partial t}+\frac{\partial\vec v}{\partial x}v_x+\frac{\partial\vec v}{\partial y}v_y+\frac{\partial\vec v}{\partial z}v_z=$$

$$=\frac{\partial\vec v}{\partial t}+\left(v_x\frac{\partial}{\partial x}+v_y\frac{\partial}{\partial y}+v_z\frac{\partial}{\partial z}\right)\vec v=\frac{\partial\vec v}{\partial t}+(\vec v\cdot\nabla)\vec v$$

[EvilPhysicist]

В. Войтик, Someone, я знаю, что $\cfrac{d\mathbf{v}}{dt}=\cfrac{\partial \mathbf{v}}{\partial t}+(\mathbf{v}\nabla )\mathbf{v} $, но не могу понять, почему это так.
Тут получается, что мы задаём поле скоростей среды и тогда действительно $ d\vec v = \cfrac{\partial v}{\partial t} dt + \cfrac{\partial v}{\partial x_k} dx_k $. Мне не понятно, почему когда мы считаем производную по времени мы читаем пространственные переменные не переменным, а функциями.

[Someone]

Мы ведь рассматриваем движение частицы жидкости. Её координаты действительно являются функциями времени.

[EvilPhysicist]

Someone в сообщении #613610 писал(а):

Мы ведь рассматриваем движение частицы жидкости. Её координаты действительно являются функциями времени.

Это уже понятно. По крайней мере с физической точки зрения.
А с математической всё ещё мутно.

[Someone]

Повторите курс математического анализа. Тему "производная сложной функции" для функций нескольких переменных.

[EvilPhysicist]

С математической точки зрения начинает доходить, но, кажется через чур сложно.

Получается мы должны взять два 3-мерных многообразия $M, S $. $M$ - "символизирует" пространство, $S$ - среду. Причём мы требуем чтобы существовало нужное число раз дифференцируемое взаимооднозначное отображение $f\colon S \to M $.

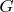
Далее, чтобы описать движение среды, надо взять однопараметрическую абелеву группу Ли $G $ элементам которой будут нужное число раз дифференцируемые взаимооднозначние отображения $f^t\colon S \to M $, обладающие групповым свойством $f^a f^b = f^{a+b} $ и кроме того множество $ \gamma_\alpha = \left\lbrace f^t \alpha\colon t \in [a,b], \alpha \in S \right\rbrace $ должно быть гладкой кривой на $M$.

Дак вот тогда, в каждой точке $M$ можно определить вектор $ \vec v(t) $ - который будет касательным вектором к кривой $\gamma_\alpha $ в данной точке. И соответственно на всём $M$ можно задать векторное поле $ \vec v(x,y,z,t) $.

И вот тут мысль обрывается. Но мне думается, что если этот формализс правильно дальше продолжить, то можно получить заветное $ \cfrac{d\vec v}{dt} = \cfrac{\partial \vec v}{\partial t} + (\vec v \nabla ) \vec v $.

-- 02.09.2012, 01:06 --

Someone в сообщении #613620 писал(а):

Повторите курс математического анализа. Тему "производная сложной функции" для функций нескольких переменных.

Там, немного не то.
Во-первых пока рассматриваем не релятивистский случай - $t$ выделенная переменная, к самому пространству никакого отношения не имеющая. И то, что я писал

EvilPhysicist в сообщении #613609 писал(а):

$ d\vec v = \cfrac{\partial v}{\partial t} dt + \cfrac{\partial v}{\partial x_k} dx_k $

это вообще глупость. Потому что в такой формализации у нас есть дивергенция векторного поля $ \nabla \vec v = \cfrac{\partial \vec v}{\partial x_k} $ и есть производная по времени $ \cfrac{d \vec v}{d \vec t} $ которые никак не связаны.
Во-вторых, на сколько я помню, если мы ищем частную производную $ \cfrac{\partial f(x,y,z)}{\partial } $ и пишем что-то вроде $ \cfrac{\partial f(x,y)}{\partial } = \cfrac{\partial f}{\partial x} + \cfrac{\partial f}{\partial y}\cfrac{\partial y}{\partial x} $, то мы должны явно задать зависимость $y=y(x) $ и таким образом мы производную посчитаем только на кривой $ y=y(x) $ но не во всём пространстве.

[Someone]

Изменение скорости в данной точке имеет две причины: непосредственная зависимость скорости от времени ($\frac{\partial\vec v}{\partial t}$) и перенос скорости движущейся частицей ($(\vec v\cdot\nabla)\vec v$).

-- Сб сен 01, 2012 23:19:39 --

EvilPhysicist в сообщении #613621 писал(а):

Во-первых пока рассматриваем не релятивистский случай

Куда-то Вас не туда понесло. Причём тут вообще разница между СТО и классической механикой? Или Вы думаете, что в классической механике нельзя ввести пространство-время? Ещё как можно! И даже ньютоновскую гравитацию можно описать на манер ОТО - искривлением пространства-времени.

[Joker_vD]

\begin{multline*}\frac{d}{dt}\vec v(t,x(t),y(t),z(t))=\\=\frac{\partial}{\partial t}\vec v(t,x(t),y(t),z(t)) + \frac{\partial}{\partial x}\vec v(t,x(t),y(t),z(t))\frac{d}{dt}x(t)+\\+\frac{\partial}{\partial y}\vec v(t,x(t),y(t),z(t))\frac{d}{dt}y(t)+\frac{\partial}{\partial z}\vec v(t,x(t),y(t),z(t))\frac{d}{dt}z(t)=...\end{multline*}

[Someone]

Да расписывал я ему это.

[EvilPhysicist]

Someone в сообщении #613630 писал(а):

Изменение скорости в данной точке имеет две причины: непосредственная зависимость скорости от времени ($\frac{\partial\vec v}{\partial t}$) и перенос скорости движущейся частицей ($(\vec v\cdot\nabla)\vec v$).

Да, с физической точки зрения это понятно. Не понятно как это правильно математически формализовать.

Someone в сообщении #613630 писал(а):

Или Вы думаете, что в классической механике нельзя ввести пространство-время? Ещё как можно! И даже ньютоновскую гравитацию можно описать на манер ОТО - искривлением пространства-времени.

Да, можно, но при этом пространство и время всё равно будут не связаны.
В том смысле, что время всё-равно будет параметром, которым вы описываете движение в пространстве.

[Someone]

EvilPhysicist в сообщении #613715 писал(а):

Не понятно как это правильно математически формализовать.

Формула полной производной.

[EvilPhysicist]

Someone в сообщении #613775 писал(а):

Формула полной производной.

Ну полную производную мы тоже считаем по кривой $(x(t),y(t),z(t)) $, а тут на надо посчитать её в каждой точке.

-- 02.09.2012, 15:18 --

Но можно сделать так.
Взять линейное пространство $\mathbb R^3$. Взять однопараметрическую группу его диффеоморфизмов его в себя $G=\left\lbrace g^t \colon \mathbb R^3 \to \mathbb R^3 \right\rbrace $. Обратное отображение к $ g^t $ обозначит $h^t $

Тогда в каждой точке можно определить вектор $\vec v(t,\vec r) = \cfrac{d}{dt} g^t (h^t(\vec r)) $.
Тогда на $\vec r$ можно смотреть как на $g^t(h^t \vec r) $. Тогда $\vec v(t,\vec r) = \vec v(t, g^t(h^t \vec r)) $ и тогда производная $ \cfrac{d}{dt} \vec v(t,\vec r) = \cfrac{\partial \vec v}{\partial t} + \cfrac{\partial \vec v}{\partial g^t(h^t \vec r)} \cfrac{\partial g^t(h^t \vec r)}{\partial t} $, что не трудно проверить даёт нужное $ \cfrac{d}{dt} \vec v = \cfrac{\partial \vec v}{\partial t} + (\vec v \nabla)\vec v $