Чё за когомология, а?

[Борис Лейкин]

Это... ну... типа... братки, чё за гомология-когомология, блин, такая? А?

[AlexDem]

Можно посмотреть, к примеру, Свитцер Алгебраическая топология - гомотопии и гомологии или Спеньер Алгебраическая топология... Подробностей не знаю пока.

[Борис Лейкин]

Так я и не понял ничего про эти когомологии.
Во ещё нашёл М. Э. Казарян. Введение в теорию гомологий PDF файл (971 Кб)

Зато узнал, что Теория Мотивов - мать всех теорий когомологий.
kea-monad.blogspot.com/search?q=motives

Цитата:

As Cartier explains, motives are a part of Grothendieck's dream, a vision of unifying number theory and modern topology, and hence almost everything else as well. The theory of motives is still mysterious, although an impressive amount of progress in the related physics and mathematics has been made in the last 30 years. Consider for example the work of Kontsevich on motives and operads in deformation quantization. It's kind of funny that the mathematicians have chosen a word (motives) that starts with M. It's their version of M-theory!

Теория Мотивов - Математическая Теория Всего! Вот как оказывается.

[Борис Лейкин]

36. (c2) В.В.Прасолов. Элементы теории гомологий

[Борис Лейкин]

Из книжки Полчинского про теорию струн.

Цитата:

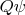
Cohomology in any vector space with a nilpotent operator Q (one such that Q^2 = 0), the kernel of Q modulo the image of Q. That is, the space of closed states (those annihilated by Q) with the exact states (those of the form $Q\psi$) defined to be equivalent to zero. De Rham cohomobgy is the cohomology of the exterior derivative d acting on differential forms. 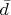On a complex manifold, Dolbeault cohomology is the cohomology of $d$ and $\bar{d}$ (the (1,0) and (0,1) parts of d) on (p, q)-forms. Homology is the cohomology of the boundary operator. BRST cohomology is the cohomology of the BRST operator, and defines the physical space of a gauge-invariant theory.

[Борис Лейкин]

Вот кстати, кому интересно, Джим Сташефф "Обзор когомологической физики"
www.math.unc.edu/Faculty/jds/survey.pdf