II тур (7.02.2007)
8 класс
1.
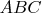

остроугольный треугольник, в котором

. Пусть


такая точка на стороне

. Далее, пусть точка

на описанной
окружности треугольника
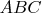
такая, что прямая

перпендикулярна
стороне
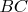
, причем точки

и

лежат по разные стороны от
прямой
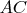
. Докажите, что прямая

перпендикулярна
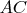
.
2.

. Найти

.
3. На доске записаны все правильные несократимые дроби со
знаменателями от 2 до 2007. Двое игроков по очереди ставят знаки

или

перед дробями (в произвольном порядке). Когда перед
всеми дробями стоят знаки, считается их сумма. Если она целая,
выигрывает тот, кто ходил последним, иначе

его оппонент. Кто
выигрывает при наилучшей игре обоих?
4. На летние каникулы 2007 года приехали отдыхать дети в лагерь.
Каждая девочка посмотрела влюбленным взглядом на каждого мальчика,
которого знала, а каждый мальчик влюбленным взглядом

на девочек,
которых не знает. Сколько было в лагере детей, если всего было
влюбленных взглядов 143, а детей

не более 40.
9 класс
1. По кругу некоторым образом расставили числа

.
Разрешается менять соседей местами. Через некоторое время все номера
оказались на позициях, диаметрально противоположных исходным.
Доказать, что хотя бы раз менялись числа, дающие в сумме 2007.
2.

,

. Доказать, что

.
3. Дан равнобедренный треугольник
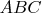
. Точка

выбрана на
стороне
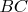
так, что

, а точка

на отрезке
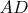

так,
что

. Докажите, что

.
4. Дана последовательность пронумерованных единичных квадратиков
бесконечной длины

Монетка находится на позиции 2.
Двое игроков по очереди двигают монетку вперед минимум на 1, но не
более, чем на 2007 позиций. Проигрывает тот, кто поставит монетку на
не простой номер. Кто выигрывает при правильной игре?
10 класс
1. В треугольнике
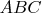
на стороне
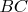
взята точка

. На отрезке

взята точка

, и проведены прямые
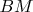
и

до пересечения
со сторонами
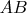
,
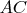
. Пусть это точки

и

. Из точки

на

опустили перпендикуляр. Найти геометрическое место точек

основ этих перпендикуляров.
2. Задана некоторая бесконечная монотонно возрастающая
последовательность чисел:

причем для всех натуральных

:

. Доказать, что
каждое натуральное число

представимо в виде

, где

,


некоторые члены последовательности.
3. Пусть

больше 1 и


количество непустых подмножеств

множества

со следующим свойством: среднее
арифметическое элементов

является целым числом. Доказать, что

всегда четно.
4. На окружности имеются красные и синие точки. Разрешается добавить
красную точку и изменить цвет ее соседей или забрать красную точку и
изменить цвет бывших соседей. Пусть сначала было две красных точки
(менее двух точек оставлять не разрешается). Можно ли получить
разрешенными операциями две синие точки?
11 класс
1. Решите в натуральных числах уравнение

, где

.
2. В треугольнике
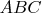
на стороне
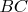
взята точка

. На отрезке

взята точка

, и проведены прямые
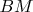
и

до пересечения
со сторонами
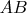
,
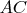
. Пусть это точки

и

. Из точки

на

опустили перпендикуляр. Найти геометрическое место точек

основ этих перпендикуляров.
3. Найдите все

, такие, что

для всех действительных

и

.
4. На окружности имеются красные и синие точки. Разрешается добавить
красную точку и изменить цвет ее соседей или забрать красную точку и
изменить цвет бывших соседей. Пусть сначала было две красных точки
(менее двух точек оставлять не разрешается). Можно ли получить
разрешенными операциями две синие точки?



