В которых Вы не в состоянии привести строгое обоснование?
Далась Вам эта строгость. Ну пожалуйста; вот
абсолютно строгое формальное обоснование примерно тех соображений, которые я приводил раньше.
Сначала -- формальная схема. Обозначим для удобства точку на стержне, за которой мы следим, через

. Пусть расстояние от этой точки до левого конца стержня есть

(оно, естественно, постоянно) и пусть

-- косинус и синус угла наклона стержня; в момент, когда точка

касается опоры, полагаем

и

. Рассмотрим небольшой сдвиг левого конца стержня на

по горизонтали. Тогда перемещение точки

-- это

.
Новая касательная пересечётся со старой где-то недалеко от

; обозначим через

расстояние от точки пересечения до

(вдоль старого положения стержня) и через
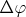
изменение угла наклона. Тогда при

:


Другими словами,

где

-- это вектор, соединяющий левый конец стержня с точкой касания. Т.е. если скорость перемещения левого конца существует и не равна нулю, то скорость перемещения точки

тоже существует, направлена вдоль стержня и мы даже знаем, чему она равна.
Что здесь нужно для корректности? Только одно: чтобы было

при

. Это мгновенно следует из строгой выпуклости верхней опоры, поскольку тогда положение точки касания непрерывно зависит от перемещения левого конца (без строгой же выпуклости просто разваливается сама формулировка задачи). А вот гладкость верхней опоры вовсе и не обязательна. (Гладкость нижней, конечно, нужна; я ограничился случаем горизонтального перемещения только чтоб не возиться с лишнми значками -- ясно, что там принципиально ничего не изменится.)
Вот так или примерно так бы я стал доказывать, будучи математиком. Однако
здесь я, будучи человеком законопослушным -- физик, и потому просто говорю, что это очевидно.
(Оффтоп)
Вы же, между прочим, непоследовательны: говорите про существование каких-то скоростей, проверить же их существование даже не удосуживаетесь. Мне (в этой ветке) такое было бы ещё простительно, но не Вам как приверженцу абсолютной строгости.