В Вашей же рекомендованной литературе на стр. 17 которую Вы очевидно не дочитали до конца
http://mmmf.msu.ru/lect/spivak/summa_sq.pdf после доказательства леммы 2, которую Эйлер действительно доказал бесконечным спуском и на которую Вы ссылаетесь, есть еще и то, что в доказательстве теоремы Ферма о простом 4к+1 Эйлер не использовал эту лемму
Где там написано, что не используется лемма 2? Вы сами пишите (и правильно), что Эйлер использовал лемму 3, но это вовсе не означает, что он не использовал лемму 2. Кстати, лемма 3 --- то же самое, что и теорема 2, только доказывается по-другому (доказательство леммы 3 именно такое, которое дал Эйлер). Вообще, различных способов доказать теорему Ферма-Эйлера придумали уже несколько десятков, включая и конструктивные (в которых предъявляются представление простого вида

суммой двух квадратов). Разберите подробно хотя бы одно доказательство.
Действительно, по-другому, без использования спуска, а применяя малую теорему Ферма(внизу стр. 17 "со слов "...Впрочем, Эйлер в 1749 году так не рассуждал ..."
То же самое говорится и в книге. Могу ошибиться с автором, (скорее всего Гарольд М. Эдвардс) Диофантов анализ в Европе ХIII - XVI вв, глава IV стр. 216 "...Заметим, что после Ферма метод спуска к утвердительным предложениям, насколько нам известно не применялся" и примечание 5 на этой же странице "Недавно предложение о том, что всякое простое число вида 4k+1 представимо суммой двух квадратов, было доказано методом спуска в книге Sharlou W., Opolke II. Fon Fermat bis Minkowski, B. etc.: Springer, 1980r
-- 16.08.2011, 22:55 --Все правильно. Но мы же доказываем из противоположного, для любого простого числа 4k+1, предполагая, что оно не составляется из двух квадратов и методом спуска приходим как раз к тем числам, о которых вы говорите (наименьшее из них 5), доказывая тем, что наше предположение неверно.
Пустые слова. Укажите конкретный способ, позволяющий, исходя из простого
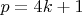
, не представимого суммой двух квадратов, построить новое простое

, которое также не представлялось бы суммой двух квадратов.
Доказательство начинается с самого элементарного, рекуррентным методом, начиная с чисел 4, 8, 12,16, показывается, что при предположении (3) не существует чисел

, таких, чтобы

составлялось бы из двух квадратов, а следовательно, существует

, меньшее

которое также не составлялось бы двумя квадратами... И все это показано в статье.