AlexMAS писал(а):
Компоненты Dxx и Dyy, если я правильно понимаю, определяют нормальные кривизны в направлении осей Ox и Oy соответственно.
Для кривизны важны еще и первые производные. Рассмотрим полуцилиндр

, ось которого параллельна

. Нормальная кривизна сечения плоскостью

всюду одна и та же, а производная

разная.
Обратный пример: параболический цилиндр

. Производная

всюду равна

, но кривизна зависит от

(легко заметить, что парабола

вблизи нуля более искривлена, чем вдали от нуля).
Поэтому лучше говорить не о нормальной кривизне, а о второй производной. Это не только

и

, но и производная по произвольному направлению -- мы ее сейчас вычислим.
AlexMAS писал(а):
Можно ли считать, что компоненты Dxy в матрице Гессе определяют нормальную кривизну в заданной точке в направлении dx·dy (то есть где-то по "диагонали" между Ox и Oy)?
Пусть вектор

, задающий направление дифференцирования в точке, получается поворотом вектора

против часовой стрелки на угол

. Тогда будем характеризовать направление этим углом

.
Найдем вторую производную по направлению

. Введем систему координат

, повернутую против часовой стрелки на угол

относительно координат
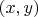
:


Координатные линии
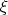
имеют как раз направление

, поэтому находим

,

.
Это и есть вторая производная функции по направлению

. Видно, что "задействованы" все вторые производные, и ни при каком

не остается только

. Поэтому

не имеет смысла второй производной по какому-то "косому" направлению.
Пример: параболический цилиндр

. Значение

не меняется в "диагональном" направлении

, но

прекрасненько отлична от нуля.

имеет такой смысл: это скорость изменения

в направлении

= скорость изменения

в направлении

. В "трехмерном" представлении это выглядит так. Возьмем на поверхности

точку

, проведем через нее плоскость, параллельную

, получится сечение -- кривая

. Угловой коэффициент касательной к ней в точке

-- это

. Теперь будем двигать точку
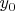
, повторяя построение. Скорость изменения углового коэффициента -- и есть смешанная производная

. Если угловой коэффициент сечения

не меняется при изменении
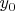
-- смешанная производная равна нулю.
Моё мнение: "трехмерные" дифференциально-геометрические аналогии были бы полезны, если бы координата

была в каком-то смысле равноценна координатам

,

. Тогда, например, имел бы смысл поворот координат или поверхности вокруг произвольной оси, и дифгеометрические инварианты работали бы в полную силу. А так -- у нас все-таки область в двумерном пространстве
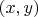
, в которой задана функция

. Тривиальное преобразование

изменит поверхность с постоянной
кривизной (сферу) в поверхность с переменной
кривизной (эллипсоид). Но оно не превратит функцию с постоянной
второй производной в функцию с переменной
второй производной.



