Здравствуйте!
(Решение узнал в университете, добавил его в данном сообщении.)Подзадача:

— вращение вокруг точки A на угол

,

— вращение вокруг точки B на угол
![$\[\psi \]$ $\[\psi \]$](https://dxdy-01.korotkov.co.uk/f/8/5/c/85cfdb7fff02a4cdb42a67c44b65bd1682.png)
. Доказать, что
![$\[\delta = {(\sigma \tau )^{ - 1}}\]$ $\[\delta = {(\sigma \tau )^{ - 1}}\]$](https://dxdy-04.korotkov.co.uk/f/3/0/f/30f0191841333702091f3289fab5261982.png)
также является вращением. Пусть C — центр данного вращения. Доказать, что углы

в два раза меньше, чем углы

, где

— угол вращения
![$\[\delta \]$ $\[\delta \]$](https://dxdy-01.korotkov.co.uk/f/8/9/7/897db2f9a92bccdf9d8d7970b7ee090482.png)
(значения углов берутся по модулю).
![$\[\begin{array}{l}
\tau \Leftrightarrow {f_1}(z) = {w_1}z - {z_1}{w_1} + {z_1}\\
\sigma \Leftrightarrow {f_2}(z) = {w_2}z - {z_2}{w_2} + {z_2}\\
{\tau ^{ - 1}} \Leftrightarrow f_1^{ - 1}(z) = w_1^{ - 1}z - {z_1}w_1^{ - 1} + {z_1}\\
{\sigma ^{ - 1}} \Leftrightarrow f_2^{ - 1}(z) = w_2^{ - 1}z - {z_2}w_2^{ - 1} + {z_2}
\end{array}\]$ $\[\begin{array}{l}
\tau \Leftrightarrow {f_1}(z) = {w_1}z - {z_1}{w_1} + {z_1}\\
\sigma \Leftrightarrow {f_2}(z) = {w_2}z - {z_2}{w_2} + {z_2}\\
{\tau ^{ - 1}} \Leftrightarrow f_1^{ - 1}(z) = w_1^{ - 1}z - {z_1}w_1^{ - 1} + {z_1}\\
{\sigma ^{ - 1}} \Leftrightarrow f_2^{ - 1}(z) = w_2^{ - 1}z - {z_2}w_2^{ - 1} + {z_2}
\end{array}\]$](https://dxdy-04.korotkov.co.uk/f/f/5/3/f534dc15e82ca4bd1bb73e84f820ec6982.png)
Так как мы рассматриваем обратную функцию от композиции двух биекций, то мы можем утверждать, что:

Это можно доказать и по-другому:

Пусть

— вращение на угол

. Тогда

.
Докажем, что

представимо в таком виде:
![$\[\begin{array}{l}
\widetilde f(z) = w_1^{ - 1}w_2^{ - 1}z + {z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1} = w_1^{ - 1}w_2^{ - 1}z + {z_3}(1 - w_1^{ - 1}w_2^{ - 1})\\
\Rightarrow {z_3}(1 - w_1^{ - 1}w_2^{ - 1}) = {z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1}\\
\Rightarrow {z_3} = \frac{{{z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1}}}{{1 - w_1^{ - 1}w_2^{ - 1}}}
\end{array}\]$ $\[\begin{array}{l}
\widetilde f(z) = w_1^{ - 1}w_2^{ - 1}z + {z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1} = w_1^{ - 1}w_2^{ - 1}z + {z_3}(1 - w_1^{ - 1}w_2^{ - 1})\\
\Rightarrow {z_3}(1 - w_1^{ - 1}w_2^{ - 1}) = {z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1}\\
\Rightarrow {z_3} = \frac{{{z_1} - {z_1}w_1^{ - 1} + {z_2}w_1^{ - 1} - {z_2}w_1^{ - 1}w_2^{ - 1}}}{{1 - w_1^{ - 1}w_2^{ - 1}}}
\end{array}\]$](https://dxdy-04.korotkov.co.uk/f/7/2/e/72e21d07d079bf3fc0d52d72e5637dde82.png)
По условию
![$\[w_1^{ - 1}w_2^{ - 1} \ne 1 \Rightarrow (1 - w_1^{ - 1}w_2^{ - 1}) \ne 0\]$ $\[w_1^{ - 1}w_2^{ - 1} \ne 1 \Rightarrow (1 - w_1^{ - 1}w_2^{ - 1}) \ne 0\]$](https://dxdy-03.korotkov.co.uk/f/a/b/2/ab28b8a623fac5c39729b6692534acc982.png)
.
Докажем, что искомое вращение есть вращение на угол

:
![$\[\begin{array}{l}
w_1^{ - 1}w_2^{ - 1} = (\cos (\varphi ) - I\sin (\varphi )) \cdot (\cos (\psi ) - I\sin (\psi )) = \\
= \cos (\varphi )\cos (\psi ) - \sin (\varphi )\sin (\psi ) - I(\sin (\varphi )\cos (\psi ) + \sin (\psi )\cos (\varphi )) = \\
= \cos (\varphi + \psi ) - I\sin (\varphi + \psi )
\end{array}\]$ $\[\begin{array}{l}
w_1^{ - 1}w_2^{ - 1} = (\cos (\varphi ) - I\sin (\varphi )) \cdot (\cos (\psi ) - I\sin (\psi )) = \\
= \cos (\varphi )\cos (\psi ) - \sin (\varphi )\sin (\psi ) - I(\sin (\varphi )\cos (\psi ) + \sin (\psi )\cos (\varphi )) = \\
= \cos (\varphi + \psi ) - I\sin (\varphi + \psi )
\end{array}\]$](https://dxdy-02.korotkov.co.uk/f/1/2/0/1203d2afd84bdc8b8503244df9d9c4e882.png)
Сдвинем систему координат таким образом, чтобы точка A стала точкой начала координат, а точка B лежала на оси абсцисс.
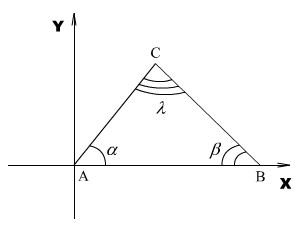
Тогда в новой системе координат

.
Вращение

.
Найдем C — центр вращения, обратного к композиции.
![$\[\begin{array}{l}
f(z) = {f_2}({f_1}(z)) = {w_1}{w_2}z - {w_2}{z_2} + {z_2}\\
{f^{ - 1}}(z) = w_1^{ - 1}w_2^{ - 1}z - w_2^{ - 1}{z_2} + {z_2}
\end{array}\]$ $\[\begin{array}{l}
f(z) = {f_2}({f_1}(z)) = {w_1}{w_2}z - {w_2}{z_2} + {z_2}\\
{f^{ - 1}}(z) = w_1^{ - 1}w_2^{ - 1}z - w_2^{ - 1}{z_2} + {z_2}
\end{array}\]$](https://dxdy-03.korotkov.co.uk/f/a/c/2/ac2504cd413482d7333e430b1b1f3a5782.png)
Представим
![$\[{f^{ - 1}}(z)\]$ $\[{f^{ - 1}}(z)\]$](https://dxdy-01.korotkov.co.uk/f/0/6/8/068740d57ac5409513ddee2f85268e7082.png)
в «каноничном виде»:
![$\[\begin{array}{l}
w_1^{ - 1}w_2^{ - 1}z - w_2^{ - 1}{z_2} + {z_2} = w_1^{ - 1}w_2^{ - 1}z - w_1^{ - 1}w_2^{ - 1}{z_0} + {z_0}\\
{z_0} = \frac{{ - w_2^{ - 1}{z_2} + {z_2}}}{{1 - w_1^{ - 1}w_2^{ - 1}}} = {z_2}\frac{{1 - w_2^{ - 1}}}{{1 - w_1^{ - 1}w_2^{ - 1}}} = x\frac{{1 - \cos \psi + I\sin \psi }}{{1 - \cos (\varphi + \psi ) + I\sin (\varphi + \psi )}} = \\
= \left| \begin{array}{l}
1 - \cos \theta = {\cos ^2}\frac{\theta }{2} + {\sin ^2}\frac{\theta }{2} - {\cos ^2}\frac{\theta }{2} + {\sin ^2}\frac{\theta }{2} = 2{\sin ^2}\frac{\theta }{2}\\
\sin \theta = 2\sin \frac{\theta }{2}\cos \frac{\theta }{2}\\
1 - \cos \psi + I\sin \psi = 2{\sin ^2}\frac{\psi }{2} + I \cdot 2\sin \frac{\psi }{2}\cos \frac{\psi }{2} = \\
2\sin \frac{\psi }{2}(\sin \frac{\psi }{2} + I\cos \frac{\psi }{2})\\
1 - \cos (\varphi + \psi ) + I\sin (\varphi + \psi ) = 2\sin \frac{{\varphi + \psi }}{2}(\sin \frac{{\varphi + \psi }}{2} + I\cos \frac{{\varphi + \psi }}{2})
\end{array} \right| = \\
= x\frac{{2\sin \frac{\psi }{2}(\sin \frac{\psi }{2} + I\cos \frac{\psi }{2})}}{{2\sin \frac{{\varphi + \psi }}{2}(\sin \frac{{\varphi + \psi }}{2} + I\cos \frac{{\varphi + \psi }}{2})}}\\
\arg {z_0} = \frac{\psi }{2} - \frac{{\varphi + \psi }}{2} = - \frac{\varphi }{2}
\end{array}\]$ $\[\begin{array}{l}
w_1^{ - 1}w_2^{ - 1}z - w_2^{ - 1}{z_2} + {z_2} = w_1^{ - 1}w_2^{ - 1}z - w_1^{ - 1}w_2^{ - 1}{z_0} + {z_0}\\
{z_0} = \frac{{ - w_2^{ - 1}{z_2} + {z_2}}}{{1 - w_1^{ - 1}w_2^{ - 1}}} = {z_2}\frac{{1 - w_2^{ - 1}}}{{1 - w_1^{ - 1}w_2^{ - 1}}} = x\frac{{1 - \cos \psi + I\sin \psi }}{{1 - \cos (\varphi + \psi ) + I\sin (\varphi + \psi )}} = \\
= \left| \begin{array}{l}
1 - \cos \theta = {\cos ^2}\frac{\theta }{2} + {\sin ^2}\frac{\theta }{2} - {\cos ^2}\frac{\theta }{2} + {\sin ^2}\frac{\theta }{2} = 2{\sin ^2}\frac{\theta }{2}\\
\sin \theta = 2\sin \frac{\theta }{2}\cos \frac{\theta }{2}\\
1 - \cos \psi + I\sin \psi = 2{\sin ^2}\frac{\psi }{2} + I \cdot 2\sin \frac{\psi }{2}\cos \frac{\psi }{2} = \\
2\sin \frac{\psi }{2}(\sin \frac{\psi }{2} + I\cos \frac{\psi }{2})\\
1 - \cos (\varphi + \psi ) + I\sin (\varphi + \psi ) = 2\sin \frac{{\varphi + \psi }}{2}(\sin \frac{{\varphi + \psi }}{2} + I\cos \frac{{\varphi + \psi }}{2})
\end{array} \right| = \\
= x\frac{{2\sin \frac{\psi }{2}(\sin \frac{\psi }{2} + I\cos \frac{\psi }{2})}}{{2\sin \frac{{\varphi + \psi }}{2}(\sin \frac{{\varphi + \psi }}{2} + I\cos \frac{{\varphi + \psi }}{2})}}\\
\arg {z_0} = \frac{\psi }{2} - \frac{{\varphi + \psi }}{2} = - \frac{\varphi }{2}
\end{array}\]$](https://dxdy-03.korotkov.co.uk/f/2/4/b/24b64da732be742745401776d392ed6182.png)
Для других углов доказывается аналогично. Отмечу, что представленная на рисунке ситуация, где C лежит именно в I четверти, не обязательно является истинной. Но сути алгебраического доказательства это не меняет, насколько видится.
Геометрическое доказательство последнего факта приведено в книге Исаака Моисеевича Яглома «Геометрические преобразования и преобразования подобия», 1955 год, I том, стр. 35—37.
Прошу прощения, что не сразу разместил формулы в TeX.