Захотелось мне что-то провести небольшую "ревизию" условия задачи. Вот, например,
paha требовал корректного определение оператора округления. Давайте попробуем подобрать что-нибудь подходящее.
Каким свойствам должен удовлетворять "округлятор"

? Понятно, что он должен оставлять неподвижными точки

, то есть действовать как метрический проектор

. Также ясно, что в общем случае

-- многозначное отображение (ой!). Кстати, далее, при работе с многозначными функциями будет подразумеваться возможность поточечного применения функции к подмножеству области определения с объединением полученных образов (вполне естественная договоренность).
Произвольности выбора алгоритма округления хорошо отвечает "округлятор" сопоставляющий точке из
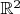
вершины содержащего её целочисленного квадратика -- фундаментального параллелограмма ортогональной

; другими словами, округлятор должен покоординатно округлять точку всеми возможными способами. Назовем такой округлятор
сильным. Сходимость траекторий при использовании сильного округлятора, сдается мне, тесно связана со структурой

, вернее, с распределением целочисленных точек на окружностях, а распределение это вовсе нетривиально, e.g. на окружности радиуса 350 лежат аж 60 таких точек и х.з., что они там делают. :) Кажется,
Sonic86 рассуждал на эту тему, так что хотелось бы от него какие-нибудь комментарии услышать...
В принципе, такой округлятор очень удобен, например, у него (в композиции с

) вроде бы нет равновесных точек. Но если удастся доказать сходимость любой траектории при использовании именно сильного округлятора, то это будет настоящим чудом!
Более же простой округлятор, -- назовем его
слабым, -- напрямую соответствует требованию округления до ближайшей точки решетки. Его можно определить или через козякиновский round или например как

Шансов сойтись у траектории слабого округлятора гораздо больше, но и сценариев такой сходимости тоже больше, что уже не так хорошо. Например эволюция системы может внезапно остановиться в некоторой точке равновесия.
Во всяком случае, предлагаю пока иметь дело именно со слабым округлятором.
В принципе, поведение системы видимо очень сильно зависит от конкретных свойств округлятора. Легко придумать похожую динамическую систему, основанную также на неточных поворотах, которая будет, к примеру, заведомо сходиться, или наоборот, расходиться, причем с очевидностью... На ум сразу же приходит проблема численного интегрирования уравнения

, при котором вместо окружностей может получиться раскручивающаяся до бесконечности спираль.
Причина расхождения траектории по спирали к бесконечности при грубом интегрировании

, например методом Эйлера, кроется в продвижении интегратора на каждом элементарном временном промежутке вдоль направленных от нуля касательных к концентрическим окружностям суть настоящим интегральным кривым этого дифура.
Конечно, это всего-лишь пример, имеющий мало общего с поворотами на решетке, при которых существенна анизотропия дискретного пространства... Так что поехали дальше. :)
Небольшое замечание. Всегда можно считать начальное состояние подмножеством решетки, ведь даже если начальная точка не принадлежит решетке, то не составит труда первую итерацию (поворот/округление) расчитать вручную.
В первую очередь мне захотелось исследовать неподвижные точки оператора

. К сожалению, эта чрезвычайно интересная тема для меня является terra incognita и мне пришлось искать подходящие теоремки и даже выдумывать кое-какие велосипеды. Мое внимание привлекла очень красивая теоремка Кнастера-Тарского о неподвижных точках монотонных отображений на решетках, в отличии от многих других подобных теорем не требующая сжимающих свойств оператора эволюции, его непрерывности или однозначности (впервые я о ней узнал совсем недавно, из небезызвестной статьи V.Deolalikar,

:) ). А так как её разбора я на этом форуме не нашел, соответствующие рассуждения-доказательства приведу прямо здесь (не удержался); может быть эти идеи и сподвигнут кого-нибудь на нормальное решение. :)
Пусть булеан над решеткой (сеткой)

будет обозначен как

; кроме того, для краткости, "переобозначим" оператор

как

, воспринимая

как отображение

в себя. Ключевым моментом является простой факт:

-- полная решетка (см.
уточнение), то есть для любого подмножества

определены супремум и инфимум через объединение и пересечение элементов, соответственно.
Функция

монотонна. Под монотонностью подразумевается свойство сохранения отношения включения:

Множество

содержит все неподвижные точки

, т.е.,

. Утверждается, что

является полной решеткой; а доказательсво выглядит примерно так. Введем ещё одно вспомогательное множество

. Для любого

выполняется

(что очевидно), а значит, в силу монотонности

, справедливо

.
По определению

, верно

; получается, что

, из чего следует

. Другими словами, все элементы

"меньше"

, то есть

-- верхняя грань

(N.B., не супремум, а просто верхняя грань). Сам же

по определению супремума является наименьшей верхней гранью и не может "превышать" любую другую верхнюю грань:

причем из определения

теперь понятно, что

Так как

, то

, а монотонность позволяет применить

к обеим частям этого выражения:

; при этом становится видно, что

. Поэтому, с учетом
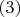
:

и, как следствие,

. Последнее выражение вместе с
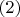
приводят к выводу о неподвижности

относительно

,

.
Понятно, что

, т.е.

содержит в том числе и все неподвижные точки

. Таким образом

является наибольшей неподвижной точкой исследуемой функции,

.
Аналогичные рассуждения можно провести и с дуальной решеткой

, которая тоже полна и на которой

тоже монотонна. В результате должен получиться симметричный вывод о существовании наименьшей неподвижной точки

где

.
Теперь несколько слов о полноте

. Зафиксируем произвольное

и выберем произвольный

. Cправедливо

, а значит и

, но так как

-- множество неподвижных точек, то

, и получается, что

, т.е.

-- верхняя грань

. Из этого вытекает

Определим отрезок

. Произвольно выберем

, при этом конечно же

. Монотонность

позволяет переписать это выражение как

, причем из последнего и из
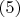
следует, что

, то есть

. Это позволяет ввести функцию

, ограничив область определения

на отрезок

(заметьте,

здесь тоже будет монотонной).
Фактически, коль скоро наш отрезок является полной решеткой, а

монотонной функцией на нем, то к этим объектам мы можем применить уже полученные выше результаты и утверждать, что согласно
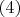
,

имеет здесь наименьшую неподвижную точку (которая является неподвижной и для

, разумеется). Так как эта точка находится на отрезке

, то она является верхней гранью для

. А раз уж она наименьшая среди всех других неподвижных точек на том же отрезке, то выходит, что найденная неподвижная точка равна

(важно помнить, что

).
Итак, произвольное

имеет супремум. Используя уже знакомый прием с применением дуальных решеток, по аналогии устанавливается существование инфимума. Значит

-- полная решетка, а из произвольности выбора этого подмножества следует полнота решетки

, в частности её непустота.
Выберем произвольное непустое подмножество

. Сконструируем оператор

, такой что

и

. Этот оператор вроде-бы обладает монотонностью:

Траекторией

будет последовательность

, в которой

, а все следующие элементы выглядят как

. Видно, что

. Монотонность

позволяет применить его к обеим частям этого выражения,

, которое теперь, очевидно, равно

. По-индукции,

Это свойство позволяет выразить предел последовательности через объединение её элементов:

Оператор

имеет ещё одно замечательное свойство -- он дистрибутивен относительно объединения:

Применим

к

:

То есть,

-- неподвижная точка

.
Внимание, положения

остро нуждаются в доказательстве и комментариях! Но это ещё пол-беды, дальше выкладки будут ещё бредовее. :)
В силу

и в свете ранее доказанного, оператор

имеет наименьшую неподвижную точку
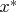
. Это можно записать как

, но можно к правой части применить

сколько угодно раз, например так:

. Очевидно, ничего не изменится если приписать к правой части символ объединения (ведь
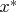
все-равно неподвижна):

Дальше интересней:

То есть, получается, что

. Вроде-бы это возможно только если

, но, как было установлено выше,

есть неподвижная точка

, а
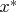
-- его наименьшая неподвижная точка. Поэтому

, т.е. монотонность на полной решетке гарантирует существование неподвижной точки, а дистрибутивность дает конструктивный способ её нахождения путем итерирования оператора

с "отталкиванием" от произвольного

.
Увы, в отжигах самого Тарского последний результат-рецепт мне найти не удалось, а у Деолаликара есть только упоминание, без объяснений (на список литературы я особо не набрасывался).
Но все равно, как вам такой аргумент по Кнастеру-Тарскому в пользу сходимости любой траектории у рассматриваемой в данной теме динамической системы? Можно ли как-нибудь развить этот подход и получить конкретные, экспериментально проверяемые параметры аттрактора, например его диаметры?



