Думаю, Вам не следует пытаться получить оценку функции распределения или плотности распределения. Посмотрите
, на который ссылаются в статье из wiki. Содержимое этого файла типичный пример применения Монте-Карло для тестирования критерия (мне только не понравился выбор значений
).
(Опишу, как можно генерировать выборки для оценки вероятности ошибки первого рода)
Для фиксированных объемов выборки, одинаковых (для простоты равных нулю) значений математических ожиданий и некоторых значений

и

. Выполняется серия экспериментов. В каждом эксперименте генерируется выборка

объема

, с параметрами
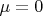
,

и выборка

объема

, с параметрами,
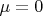
,

.
Для этих выборок находят оценки математического ожидания

,

(обозначим через

и

) и несмещенные оценки дисперсий

и

(обозначим через

и

). Далее вычисляется значение статистики

и

, здесь

округленное до целого значение приведенной Вами статистики. Проверяется условие

, где

— квантиль уровня

распределения Стьюдента с

степенями свободы. Если условие выполнено, то увеличивается на 1 счетчик случаев, когда гипотеза была отвергнута. Обычно для каждого эксперимента выполняется несколько проверок с различными уровнями. После выполнения всех экспериментов значения счетчиков делят на число экспериментов в серии.
Пример программы на Borland Pascal (компилировалось и выполнялось в среде Delphi 5.0, но использованы средства языка, имеющиеся и в более ранних диалектах Borland Pascal).
Код:
program welch;
uses NormRnd; {Модуль содержит генератор нормального распределения,
{в тексте это функции InitN1DRnd(0, 1) и N1DRnd}
const
n1 = 5;
n2 = 5;
Rep = 1000000;
sigma1 = 1;
sigma2 = 16;
var
quantile : array [1..100] of record l_80, l_90, l_95, l_99 : Extended; end;
i, j : Integer;
X: array[1..n1] of Extended;
Y: array[1..n2] of Extended;
m1, m2, ss1, ss2, t, nu: Extended;
scount_80, scount_90, scount_95, scount_99: Integer;
wcount_80, wcount_90, wcount_95, wcount_99: Integer;
txt: Text;
begin
Assign(txt, 'student.dat'); {Из файла 'student.dat' считываются квантили распределения Стюдента}
Reset(txt); {уровня 0.80, 0.90, 0.95, 0.99 и степенях свободы 1..100}
for i:= 1 to 100 do with quantile[i] do Readln(txt, l_80, l_90, l_95, l_99);
Close(txt);
scount_80:= 0; scount_90:= 0; scount_95:= 0; scount_99:= 0;
wcount_80:= 0; wcount_90:= 0; wcount_95:= 0; wcount_99:= 0;
InitN1DRnd(0, 1); {Инициализируем для получения стандартных нормальных случайных величин}
for j := 1 to Rep
do begin
m1:= 0; for i:= 1 to n1 do begin X[i]:= sigma1*N1DRnd; m1:= m1 + X[i]; end; m1:= m1/n1;
m2:= 0; for i:= 1 to n2 do begin Y[i]:= sigma2*N1DRnd; m2:= m2 + Y[i]; end; m2:= m2/n2;
ss1:=0; for i:= 1 to n1 do ss1:= ss1 + sqr(X[i] - m1); ss1:= ss1/(n1-1);
ss2:=0; for i:= 1 to n2 do ss2:= ss2 + sqr(Y[i] - m2); ss2:= ss2/(n2-1);
ss1:= ss1/n1; ss2:= ss2/n2;
t := (m1-m2)/sqrt(ss1 + ss2);
nu:= sqr(ss1 + ss2)/(sqr(ss1)/(n1-1) + sqr(ss2)/(n2-1));
with Quantile[n1+n2-2]
do begin
if t > l_80 then inc(scount_80);
if t > l_90 then inc(scount_90);
if t > l_95 then inc(scount_95);
if t > l_99 then inc(scount_99);
end;
with Quantile[Round(nu)]
do begin
if t > l_80 then inc(wcount_80);
if t > l_90 then inc(wcount_90);
if t > l_95 then inc(wcount_95);
if t > l_99 then inc(wcount_99);
end;
end;
if ParamCount > 0 {если указан параметр командной строки}
then begin {то считаем, что задано имя файла и выводим в этот файл}
Assign(txt, ParamStr(1));
Rewrite(txt);
Writeln(txt, 's: ', scount_80/Rep:8:3, scount_90/Rep:8:3, scount_99/Rep:8:3, scount_99/Rep:8:3);
Writeln(txt, 'w: ', wcount_80/Rep:8:3, wcount_90/Rep:8:3, wcount_99/Rep:8:3, wcount_99/Rep:8:3);
Close(txt);
end
else begin
writeln('s: ', scount_80/Rep:8:3, scount_90/Rep:8:3, scount_95/Rep:8:3, scount_99/Rep:8:3);
writeln('w: ', wcount_80/Rep:8:3, wcount_90/Rep:8:3, wcount_95/Rep:8:3, wcount_99/Rep:8:3);
end;
end.
В качестве примера использования такого подхода
Для случая

,

,

,

получим значения
s: 0.200; 0.100; 0.050; 0.010
w: 0.197; 0.097; 0.047; 0.008
Для случая

,

,

,

получим значения
s: 0.212; 0.117; 0.068; 0.022
w: 0.200; 0.100; 0.050; 0.010
Видно, что при большом различии дисперсий вероятность ошибки первого рода критерия Стьюдента превышает номинальные значения, с другой стороны, видно, что критерий Welch является консервативным.



