Здравствуйте, предлагаю вашему вниманию небольшую попытку простого (основанного на школьной математике), не использующего компьютер, и чрезвычайно компактного (если со всеми рюшечками, то печатная страница) "доказательства" известной теоремы о четырех красках (ныне уже доказанной жутким способом). Надеюсь услышать какие-нибудь отзывы, критику, и т.д. Слишком серьезно не воспринимайте, но на ошибки укажите, если кому не лень конечно. :)
Если что, ссылка на дядю Мишу (т.е., на меня) обязательна. :)
Формулировка (на всякий случай). Вершины планарного графа можно раскрасить всего четырьмя красками так, чтобы смежные вершины имели различные цвета.Поводом к написанию этого сообщения послужило обсуждение в соседней, созданной участником
iig, теме
Проблема 4-краски простой подход (советую предварительно ознакомиться с ней). Сразу предупрежу, что на самом деле никакого строго доказательства у меня нет, а есть лишь аппелирующие к интуиции наброски и размытые рассуждения, которыми я, собственно, и хотел поделиться в этой теме... Поэтому, если у кого-то имеется "аллергия" на попытки нематематиков что-то доказывать, то дальше лучше не читать... :) Остальным же придется переварить все нижеследующее.
Итак, пусть имеется граф

, при этом множество

содержит вершины графа, а множество

-- его ребра. Существенно, что граф неориентирован, другими словами, если

для некоторых

, то и

.
Необходимо доказать/показать/убедить, что для любого планарного

существует правильно раскрашивающее отображение
![$\varphi\colon\mathcal{V}(\Gamma)\to[1;\ 4]\subset\mathbb{N}$ $\varphi\colon\mathcal{V}(\Gamma)\to[1;\ 4]\subset\mathbb{N}$](https://dxdy-01.korotkov.co.uk/f/8/6/6/86675a0bb9d9a7d198be6299654688c482.png)
при котором выполняется
![$\forall\ u,\ v\in\mathcal{V}(\Gamma)\ \left[u\neq v\land(u,\ v)\in\mathcal{E}(\Gamma)\Rightarrow\varphi(u)\neq\varphi(v)\right]$ $\forall\ u,\ v\in\mathcal{V}(\Gamma)\ \left[u\neq v\land(u,\ v)\in\mathcal{E}(\Gamma)\Rightarrow\varphi(u)\neq\varphi(v)\right]$](https://dxdy-02.korotkov.co.uk/f/1/3/9/1392512d1ae640b0147441ca985f1ace82.png)
.
Далее будет показано, что требуемая правильная 4-раскраска может быть легко осуществлена почти для любого (в смысле отсутствия у меня контрпримеров) планарного графа (а может быть и для всех планарных графов, это зависит от правильности моих рассуждений).
Но сначала опишу основную идею; правда, дабы не спугнуть читателей её наивностью, придется начать с некоторых определений и предположений, причем я ограничусь лишь самыми необходимыми понятиями.
Определение 1. Стягивание ребра есть отождествление соединенных им вершин (с необходимым перенаправлением инцидентных им ребер).Введем функцию

возвращающую набор инцидентных ребер для любой вершины

.
Определение 2. Склейкой двух несмежных вершин называется отождествление этих вершин, то есть стягивание фиктивного ребра, добавленного между ними. Более формально, для графа  склейкой вершин
склейкой вершин  обзовем преобразование
обзовем преобразование  , конструирующее множества вершин и ребер нового графа
, конструирующее множества вершин и ребер нового графа  по формулам
по формулам ![$$\begin{align}\mathcal{E}(\Gamma') & = \mathcal{E}(\Gamma)\cup\left[\bigcup_{(a,\ u)\in \mathcal{R}_\Gamma(u)}\Big\{(a,\ v),\ (v,\ a)\Big\}\right]\setminus\mathcal{R}_\Gamma(u),\\ \mathcal{V}(\Gamma') & = \mathcal{V}(\Gamma)\setminus\{u\}.\end{align}$$ $$\begin{align}\mathcal{E}(\Gamma') & = \mathcal{E}(\Gamma)\cup\left[\bigcup_{(a,\ u)\in \mathcal{R}_\Gamma(u)}\Big\{(a,\ v),\ (v,\ a)\Big\}\right]\setminus\mathcal{R}_\Gamma(u),\\ \mathcal{V}(\Gamma') & = \mathcal{V}(\Gamma)\setminus\{u\}.\end{align}$$](https://dxdy-03.korotkov.co.uk/f/2/d/b/2dbd79ec654ec457a20a4097335ad31b82.png)
N.B., Для планарного

и несмежных

,

, если

, то верно

; это соглашение пригодится в дальнейшем.
Лемма 1. Если в планарном графе содержится более четырех вершин, то среди них найдется хотя-бы одна пара несмежных.Набросок доказательства. Если несмежных вершин в графе нет, значит граф полный. Однако известно, что максимальный полный планарный граф есть

, i.e., полный граф с большим количеством вершин заведомо непланарен. Методом от противного, доказано (хотя и так было очевидно).
 Определение 3. Склейка называется правильной если для планарного
Определение 3. Склейка называется правильной если для планарного  и некоторых двух его несмежных вершин
и некоторых двух его несмежных вершин  и
и  результирующий граф
результирующий граф  -- планарен. Сами же такие вершины называются правильно склеиваемыми.Лемма 2. В произвольном планарном 5-вершиннике найдется пара правильно склеиваемых вершин.Набросок доказательства.
-- планарен. Сами же такие вершины называются правильно склеиваемыми.Лемма 2. В произвольном планарном 5-вершиннике найдется пара правильно склеиваемых вершин.Набросок доказательства. Можно просто выполнить непосредственную проверку всех планарных пятивершинных графов. :) Но, в-принципе, можно попробовать привести такой довод. Лемма 1 говорит нам, что в пятивершинном графе найдется пара несмежных вершин. Их склейка даст 4-вершинник. Поэтому вопрос ставится так: а всякий ли 4-вершинник планарен? Ответ на него, кажется, положителен, что немедленно влечет за собой правильность склейки.
 Гипотеза 1 (усиление леммы 2). Если
Гипотеза 1 (усиление леммы 2). Если  планарен и
планарен и  , то в
, то в  существует пара правильно склеиваемых вершин.Набросок доказательства.
существует пара правильно склеиваемых вершин.Набросок доказательства. Здесь уместна индуктивная схема, которую я намечу, пошагово описав простой алгоритм.
Алгоритм 1.- Заведем список удаленных вершин
 и проинициализируем его:
и проинициализируем его:  .
. - Введем временную копию графа
 . N.B.: здесь и далее, под присваиванием графов понимается присваивание вершин и ребер, т.е.,
. N.B.: здесь и далее, под присваиванием графов понимается присваивание вершин и ребер, т.е.,  означает
означает  .
. - Если
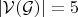 , то с применением леммы 2 алгоритм завершается.
, то с применением леммы 2 алгоритм завершается. - Найдем
 , что всегда возможно в силу леммы 1.
, что всегда возможно в силу леммы 1. - Восстановим ранее удаленные вершины и ребра:
 .
. - Произведем склейку вершин
 и
и  :
:  .
. - Если
 планарен, то завершаем алгоритм.
планарен, то завершаем алгоритм. - Добавим вершину
 в список удаленных вершин:
в список удаленных вершин:  .
. - Удалим из
 вершины
вершины  вместе с инцидентными им ребрами:
вместе с инцидентными им ребрами: 
Очевидно, что  -- планарен.
-- планарен. - Присвоим
 и вернемся к шагу 3.
и вернемся к шагу 3.
По-сути, выше был приведен алгоритм поиска правильно склеиваемых вершин в планарном графе. Видно, что алгоритм всегда завершается успешно (на каждой итерации мы удаляем одну вершину, что приводит нас в конечном счете к уже исследованному 5-вершиннику).
 Определение 4. Протоколом сжатия графа
Определение 4. Протоколом сжатия графа  назовем последовательность
назовем последовательность  из четверок
из четверок  , где
, где  - просто булеан.Определение 5. Сжатием графа
- просто булеан.Определение 5. Сжатием графа  называется применение к нему алгоритма сжатия (см. ниже).
называется применение к нему алгоритма сжатия (см. ниже).Пусть дан планарный граф

и

.
Алгоритм 2 (алгоритм сжатия).- Создадим временный граф
 .
. - Введем счетчик
 .
. - Если
 , то завершаем алгоритм.
, то завершаем алгоритм. - Гипотеза 1 гарантирует, что в
 существует пара правильно склеиваемых вершин. Пусть ими будут вершины
существует пара правильно склеиваемых вершин. Пусть ими будут вершины  .
. - Занесем в протокол выбранные вершины и их окружение (инцидентные ребра):
 .
. - Склеим выбранные вершины:
 . Важно заметить, что по определению склейки теперь
. Важно заметить, что по определению склейки теперь  , но
, но  .
. - Инкрементируем
 , присваиваем
, присваиваем  и переходим к шагу 3.
и переходим к шагу 3.
Очевидно, что алгоритм всегда завершается. При этом

содержит количество записей в протоколе

, а

. Ни протокол, ни результирующий граф не выбрасываем, ещё пригодятся. :)
Введем раскрашивающий "вектор" с компонентами

индексируемыми вершинами графа

(того самого, который планарен и содержит более четырех вершин), т.е.
![$\varrho_x\in[1;\ 4]\subset\mathbb{N},\ x\in\mathcal{V}(\Gamma)$ $\varrho_x\in[1;\ 4]\subset\mathbb{N},\ x\in\mathcal{V}(\Gamma)$](https://dxdy-02.korotkov.co.uk/f/5/2/9/5291ae502968bdde1561b87e7e97976582.png)
. Фактически,

является функцией
![$\mathcal{V}(\Gamma)\to[1;\ 4]$ $\mathcal{V}(\Gamma)\to[1;\ 4]$](https://dxdy-01.korotkov.co.uk/f/c/f/4/cf4fd03d786eefff2cbe772d01015c7e82.png)
, но строится динамически с помощью раскрашивающего алгоритма (см. ниже).
Мы используем старый граф

, который использовался в алгоритме 2. Кроме того, как уже было сказано ранее, используем результаты работы этого алгоритма, а именно 4-вершинник

(N.B., он может быть как полным, так и неполным), число

(длину протокола) и сам протокол

.
Алгоритм 3 (раскрашивающий алгоритм).- Произведем правильную раскраску графа
 с помощью вектора
с помощью вектора  . Теперь верно
. Теперь верно ![$\forall a\in\mathcal{V}(\mathcal{G})\ \varrho_a\in[1;\ 4]$ $\forall a\in\mathcal{V}(\mathcal{G})\ \varrho_a\in[1;\ 4]$](https://dxdy-02.korotkov.co.uk/f/d/9/b/d9becba36c3d062b44dc83fd2841b53a82.png) и
и ![$\forall a,\ b\in\mathcal{V}(\mathcal{G})\ \big[a\neq b\land(a,\ b)\in\mathcal{E}(\mathcal{G})\Rightarrow\varrho_a\neq\varrho_b\big]$ $\forall a,\ b\in\mathcal{V}(\mathcal{G})\ \big[a\neq b\land(a,\ b)\in\mathcal{E}(\mathcal{G})\Rightarrow\varrho_a\neq\varrho_b\big]$](https://dxdy-04.korotkov.co.uk/f/f/8/0/f805c7686a2cd734d077daa84c7e488882.png) .
. - Если
 , то завершаем работу алгоритма.
, то завершаем работу алгоритма. - Декремент
 .
. - Прочитаем последнюю запись протокола:
 , здесь
, здесь  ,
,  -- вершины из
-- вершины из  , а
, а  ,
,  -- наборы инцидентных им ребер. Заметим, что
-- наборы инцидентных им ребер. Заметим, что  по определению склейки уже принадлежит
по определению склейки уже принадлежит  .
. - Восстановим структуру графа, пользуясь текущей записью протокола. Для этого сначала добавим в граф ранее удаленную вершину
 :
:  .
. - Затем удалим ребра, инцидентные вершине
 :
:  .
. - Наконец, восстановим старые ребра вершин
 и
и  :
: 
- Логика алгоритма 2 гарантирует, что
 , а так как вершина
, а так как вершина  уже раскрашена (см. шаг 4 настоящего алгоритма), то мы можем раскрасить
уже раскрашена (см. шаг 4 настоящего алгоритма), то мы можем раскрасить  в тот же цвет:
в тот же цвет:  .
. - Переход к шагу 2.
Гипотеза 2. Раскраска  -- правильная.Набросок доказательства.
-- правильная.Набросок доказательства. Проанализируем алгоритм. Он всегда завершается, граф

совпадает с изначальным графом

. Также легко видеть, что абсолютно все вершины оказываются раскрашенными. Действительно, начальный 4-вершинник полностью раскрашен (см. шаг 1), а алгоритм добавляет к нему в дальнейшем все недостающие вершины (см. шаг 5) и каждой приписывает цвет (см. шаг 8).
Кстати о шаге 8. Этот шаг очень прост, но его последствия туманны и здесь безусловно требуются пояснения. Проблема вот в чем. Конечно, алгоритм 2 обеспечивает несмежность рассматриваемых на этом шаге вершин (

и

), поэтому им вполне законно приписывается одинаковый цвет. Но опасность кроется в шаге 7. Именно, на шаге 7 алгоритма 3 мы вслепую снабжаем новую (восстановленную) вершину

ранее имевшимися у неё ребрами рискуя вызвать конфликт цветов (вместе с тем заметим, что операции с ребрами, инцидентными вершине

, выполняются без нехороших последствий, ибо ограничиваются лишь удалением некоторых ребер без добавления новых).
Разгадка может быть такой. Изначально, т.е., на шаге 1, граф раскрашен правильно и нам достаточно показать, что правильность раскраски поддерживается в любой момент работы алгоритма. Предположим, что на произвольной итерации, до выполнения опасного шага 8, раскраска является правильной. Исходя из этого предположения мы можем сделать заключение об отсутствии конфликтов цветов между вершиной

и всеми смежными с нею вершинами. Теперь необходимо уяснить, что по определению склейки вершин

и

, операция ей обратная (т.е., операция восстановление вершины по записям протокола), по-сути, всего-лишь перенаправляет некоторые ребра, ранее инцидентные вершине

, на вершину

, которая до этого вовсе не имела ребер (см. шаг 5). А коль скоро эти перенаправляемые ребра не нарушали правильности раскраски будучи инцидентными с вершиной

, то и после присоединения к

, имеющей тот же цвет, что и

, они тоже не будут нарушать раскраски.
В последнем абзаце вроде-бы можно усмотреть доказательство по индукции, там вам и база и шаг... Но это очень мутный момент и требует дальнейшей проработки...
В остальном же, всё вроде-бы в порядке.

Для пущего понимания всего вышеизложенного рекомендую вооружиться клочками бумаги и четырьмя разноцветными хреньками с целью проследить ход моих мыслей на каком-нибудь простом практическом примере (применив алгоритмы 2 и 3). :) Также можно и программульку написать, хотя она, предположительно, будет весьма тормознутой для больших политических карт (сложно спрятаться от экспоненциальной асимптотики)...
Резюме.
Собственно, как и обещал, озвучиваю основную идею. Если на карте какие-то страны находятся достаточно далеко друг от друга, другими словами, не являются соседними государствами, то они потенциально могут иметь один и тот же цвет. Если такие страны удастся объединить в союз (и в этом моя идея перекликается с идеей
iig'а), то можно будет продолжить раскраску полученной карты, содержащей государств на одно меньше. Повторяя этот процесс мы должны неминуемо прийти к карте, на которой изображены попарно-соседние страны, на раскраске которых уже сэкономить невозможно. Если бы удалось доказать, что любая карта в результате такого процесса сводится к карте, содержащей не более четырех стран, то это могло бы быть одновременно и доказательством 4CT, так как правильно раскрасив такую предельную карту, мы можем вновь преобразовать её к изначальной, сохранив при этом правильность раскраски (ранее объединившиеся союзники ссорятся и снова становятся независимыми странами, но цвета свои продолжают помнить). Основная муть заключается именно в вопросе о возможности безболезненного распада союзов...
Что имеем в итоге? Есть парочка алгоритмов, раскрашивающих произвольную полит. карту. Совокупность доводов, приведенных в доказательство отдельных неясных моментов, позволяет надеяться на правильность такой раскраски, то есть надеяться на то, что соседи имеют различные цвета и всего в палитре их не более четырех...
![\framebox[1.1\width]{qed} \framebox[1.1\width]{qed}](https://dxdy-04.korotkov.co.uk/f/3/a/a/3aa5fd1a653cee0563dd5bc5fb010cd782.png)
Как говорится, спасибо за внимание! :) Главный вопрос-просьба у меня такой: найдите фатальную ошибку (я её, кажется, уже нашел, но не выкидывать же писанину). :)