В принципе для любых функций удовлетворяющих условиям

предел равен единице.
Графики функций из нуля выходят параллельно диагонали

, а графики обратных функций - отражены относительно этой диагонали.
Теперь можно заметить, что верхняя разность - длина вертикального отрезка от

до

, а нижняя разность - длина вертикального отрезка от

до
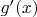
, что тоже самое, что и длина горизонтального отрезка от

до

. Т.к. производные равны единице, то

, и, опять же из-за того, что производные равны единице, длины этих отрезков тоже приблизительно равны. Т.е. предел равен единице.