К сожалению, доказательство длинно. Оно сводится главным образом к рассмотрению различных комбинаций

:
1.

имеет множители с
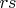
, а

- только с

или только с

. Для каждого такого случая рассматривается равенство

.
И так для каждого случая доказывается, что решений нет. Я проделывал однажды эту работу, если надо - могу повториться.
Что касается второго случая:

то да, я его пропустил. Но не умышленно. Дело в том, что

четно. Откуда

и

одинаковой четности. Если они оба четны, то получаем тривиальный случай. Поэтому они оба нечетны.
Но тогда

, откуда

.

. Т.е.

оба нечетны. Но тогда

. Что противоречит предположению о том, что числа

и

оба нечетны.