Хочется найти метод решения задач такого типа(где с одной стороны логорифм,с другой подобное выражение с x):

Всё получилось,кроме того что в конечном
равносильном неравенстве есть кусок:

Корни

и
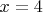
видны и интуинтивно понятно,что других корней нет,
как это доказать?
P.S. Ответ приведенный в прошлый раз просто неверный,из-за

и континуума других значений.Поэтому вопрос принципиально другой.