Бесконечно ли множество мыстамарных чисел?

[gipokrat]

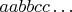
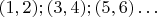
Натуральное число $n$ назовём мыстамарным (от «Мы с Тамарой ходим парой»), если в десятичной записи числа $n^2+2$ цифры идут парами: $aabbcc\dots$ (цифры $a, b, c, \dots$ не обязательно различны), то есть на местах $(1, 2); (3, 4); (5, 6)\dots$ стоят одинаковые цифры (нумеруем цифры слева направо, начиная с 1).

Перед вами первые 6 мыстамарных чисел: 3, 8, 47, 58, 334997, 8781297.

Их квадраты, увеличенные на 2 выглядят так: 11, 66, 2211, 3366, 112222990011, 77111177002211.

Создаётся ощущение, что мыстамарных чисел бесконечно много. Можно ли это доказать или опровергнуть?

[gris]

Интересно, что если нарисовать $1$, потом $2k+1$ девяток, а потом $7$, то в целевом числе в конце будет $k$ пар:
$197 \to 38811$

$19997 \to 399880011$

$19999999997 \to 399999999880000000011$

Жаль, что начало подкачало. Но доказать невозможность построения будет, наверное, трудновато. Как и найти следующий положительный пример

$3333499997 \to 11112222229999000011$ и даже

$33333333333349999999999997 \to 1111111111112222222222222299999999999900000000000011$

А тут уже виден паттерн! И даже луч!!!

[ozheredov]

gris в сообщении #1712408 писал(а):

И даже луч!!!

Симметричные кортежи можно искать? Какой там VALIDS?

[gris]

Ну если по чесноку, то надо паттерн расписать алгебраически, возвести в квадрат, прибавить 2 и показать, что результат этот самый. Типа если i натуралка, то предмыста будет
$ k=5\cdot 10^{2i+1}-3+(10^{2i}-1)/3\cdot10^{2i+2}$

Должна получиться такая мыста:
$ m=k^2+2=10^{4i+2}-10^{2i+2}+11+ (10^{2i+2}-1)/9\cdot2\cdot10^{4i+2}+ (10^{2i}-1)/9\cdot10^{6i+4}$

И чего с этим делать? Упростить? Попробовать несколько разных i и визуально убедиться, но это же не может способствовать в самый раз Я сдаюсь, хотя уверен

[gevaraweb]

Chat GPT доказал ММИ, что таких чисел бесконечно много, и на основе док-ва предложил порождающий алгоритм и программу.
С его помощью я построил пары

9983043947 -> 99661166447733338811
99614238947 -> 9922996600990011668811

[gevaraweb]

gevaraweb в сообщении #1712440 писал(а):

Chat GPT доказал ММИ,

Хотя он тот еще зведобол, выкладки я не проверял, он мне еще доказал (что неверно при $k = 1$ ):

Chat GPT писал(а):

$\paragraph{1) Вывод}$
Для каждого $k \ge 1$ число

$\[ n_k = \underbrace{33\ldots3}_{k}\,4\,\underbrace{99\ldots9}_{k}\,7 \]$
является мыстамарным, и поэтому мыстамарных чисел (как минимум) бесконечно много.

Как минимум

[gris]

Кстати, а как можно невручную доказать тождество выражений натурального аргумента? Я засунул разность в вольфрам и получил 0. Но корректно ли это и не надо ли произносить дополнительные заклинания?
(10^{4n+2}-10^{2n+2}+11+ (10^{2n+2}-1)/9\cdot2\cdot10^{4n+2}+ (10^{2n}-1)/9\cdot10^{6n+4})-(5\cdot 10^{2n+1}-3+(10^{2n}-1)/3\cdot10^{2n+2})^2-2
Result 0