|
|
Можно посчитать статистику по каждому простому до 2^20 -- сколько раз на него что-нибудь разделилось, сколько раз оно прервало проверку и т.п. Исходя из этого, можно заранее поменять порядок следования простых в таблице простых и делить сперва на самые ходовые, обеспечивая ещё более ранний выход. Теория говорит что получится список возрастающих простых - как уже и есть. Потому что m взаимно простое с любым простым больше 53 и значит остатки по таким простым от n распределены равномерно и значит остаток 0 встречается не чаще других и значит вероятность его обнаружить равна 1/p для простого p. Практика прекрасно согласуется с теорией (штуки на миллион): ...
frq=matrix(100,100);
for(i=0,oo,
...
forprime(p=59,100,
frq[p,(n+#v-1)%p+1]++;
);
);
forprime(p=59,100,printf("%2u: %6u\n",p,frq[p,1..p]);); 59: [ 16943, 16960, 16948, 16946, 16944, 16959, 16944, 16947, 16946, 16939, 16967, 16953, 16957, 16945, 16943, 16947, 16943, 16951, 16958, 16954, 16951, 16952, 16947, 16955, 16950, 16961, 16933, 16949, 16945, 16933, 16960, 16952, 16951, 16968, 16949, 16935, 16951, 16940, 16943, 16956, 16933, 16950, 16952, 16933, 16946, 16951, 16948, 16956, 16940, 16934, 16942, 16946, 16953, 16959, 16958, 16954, 16963, 16961, 16946]
61: [ 16363, 16401, 16399, 16375, 16394, 16389, 16390, 16393, 16393, 16402, 16383, 16395, 16394, 16383, 16397, 16395, 16395, 16394, 16385, 16384, 16398, 16388, 16378, 16395, 16386, 16397, 16395, 16396, 16395, 16388, 16395, 16396, 16389, 16401, 16387, 16397, 16388, 16401, 16402, 16400, 16393, 16385, 16397, 16399, 16407, 16393, 16392, 16385, 16390, 16390, 16411, 16405, 16392, 16384, 16392, 16406, 16391, 16401, 16395, 16410, 16406]
67: [ 14929, 14919, 14926, 14919, 14939, 14927, 14918, 14926, 14926, 14938, 14907, 14911, 14931, 14922, 14919, 14929, 14916, 14927, 14936, 14924, 14924, 14918, 14937, 14917, 14924, 14924, 14926, 14923, 14915, 14926, 14932, 14921, 14932, 14925, 14921, 14919, 14942, 14944, 14931, 14919, 14921, 14927, 14925, 14933, 14917, 14923, 14922, 14928, 14912, 14926, 14934, 14929, 14921, 14926, 14916, 14920, 14932, 14929, 14931, 14930, 14920, 14932, 14938, 14916, 14935, 14926, 14922]
71: [ 14077, 14088, 14093, 14083, 14081, 14080, 14080, 14085, 14075, 14091, 14092, 14081, 14087, 14078, 14083, 14083, 14090, 14096, 14073, 14083, 14080, 14075, 14092, 14076, 14071, 14092, 14096, 14077, 14079, 14088, 14080, 14086, 14084, 14096, 14085, 14104, 14092, 14069, 14074, 14070, 14087, 14065, 14095, 14079, 14095, 14085, 14085, 14073, 14071, 14096, 14089, 14086, 14088, 14098, 14084, 14078, 14086, 14095, 14097, 14088, 14072, 14082, 14101, 14099, 14081, 14085, 14079, 14084, 14086, 14079, 14087]
73: [ 13697, 13695, 13706, 13703, 13690, 13689, 13690, 13693, 13691, 13686, 13708, 13703, 13692, 13694, 13690, 13694, 13694, 13712, 13699, 13696, 13711, 13695, 13696, 13704, 13693, 13695, 13700, 13705, 13700, 13711, 13711, 13703, 13703, 13690, 13692, 13696, 13699, 13695, 13705, 13702, 13697, 13695, 13700, 13707, 13705, 13698, 13691, 13713, 13690, 13698, 13693, 13701, 13720, 13690, 13693, 13695, 13710, 13704, 13706, 13701, 13694, 13708, 13688, 13697, 13694, 13706, 13689, 13711, 13687, 13717, 13694, 13684, 13696]
79: [ 12673, 12659, 12658, 12663, 12650, 12653, 12659, 12658, 12671, 12670, 12664, 12652, 12661, 12657, 12653, 12646, 12648, 12659, 12662, 12652, 12661, 12665, 12662, 12656, 12642, 12663, 12671, 12666, 12640, 12661, 12649, 12648, 12672, 12649, 12666, 12657, 12658, 12664, 12665, 12659, 12641, 12650, 12662, 12653, 12662, 12676, 12668, 12651, 12665, 12658, 12652, 12649, 12650, 12650, 12655, 12644, 12672, 12648, 12651, 12651, 12652, 12648, 12660, 12671, 12649, 12657, 12643, 12661, 12658, 12651, 12670, 12658, 12663, 12678, 12669, 12669, 12657, 12674, 12662]
83: [ 12051, 12058, 12052, 12047, 12055, 12050, 12044, 12056, 12039, 12045, 12047, 12051, 12044, 12035, 12049, 12044, 12035, 12063, 12032, 12032, 12045, 12059, 12058, 12055, 12053, 12042, 12045, 12042, 12050, 12043, 12065, 12042, 12064, 12042, 12051, 12042, 12060, 12031, 12041, 12036, 12049, 12044, 12051, 12046, 12053, 12037, 12053, 12050, 12046, 12054, 12051, 12040, 12043, 12043, 12052, 12062, 12065, 12053, 12038, 12063, 12055, 12050, 12054, 12044, 12067, 12060, 12045, 12056, 12052, 12046, 12034, 12062, 12047, 12043, 12056, 12051, 12044, 12035, 12028, 12058, 12038, 12044, 12043]
89: [ 11242, 11229, 11232, 11237, 11242, 11233, 11232, 11233, 11242, 11249, 11240, 11249, 11234, 11221, 11231, 11232, 11242, 11233, 11243, 11224, 11230, 11243, 11245, 11227, 11237, 11245, 11246, 11234, 11244, 11232, 11232, 11228, 11243, 11233, 11230, 11234, 11232, 11237, 11239, 11243, 11241, 11243, 11236, 11241, 11235, 11249, 11241, 11244, 11236, 11234, 11235, 11228, 11238, 11248, 11236, 11227, 11232, 11236, 11237, 11253, 11240, 11230, 11234, 11243, 11235, 11224, 11222, 11220, 11236, 11227, 11221, 11228, 11253, 11232, 11251, 11250, 11225, 11223, 11226, 11227, 11238, 11232, 11226, 11249, 11228, 11242, 11245, 11239, 11230]
97: [ 10301, 10303, 10321, 10322, 10298, 10307, 10301, 10301, 10318, 10305, 10315, 10319, 10316, 10311, 10302, 10307, 10306, 10311, 10333, 10319, 10293, 10300, 10293, 10315, 10304, 10307, 10307, 10297, 10315, 10317, 10302, 10317, 10316, 10314, 10321, 10309, 10323, 10310, 10305, 10309, 10304, 10309, 10313, 10310, 10309, 10310, 10326, 10310, 10310, 10314, 10301, 10297, 10310, 10310, 10304, 10307, 10313, 10315, 10307, 10316, 10321, 10312, 10321, 10313, 10320, 10312, 10307, 10315, 10310, 10317, 10304, 10301, 10306, 10319, 10301, 10291, 10293, 10319, 10303, 10301, 10307, 10309, 10303, 10302, 10314, 10291, 10314, 10324, 10314, 10312, 10318, 10310, 10299, 10305, 10298, 10304, 10305] Соответственно на интервалах превышающих произведение проверяемых простых все комбинации остатков по всем проверяемым простым равновероятны. И если бы все вероятности разделиться на простое были одинаковы, то равновероятно на каком из них наберётся nf==nu, но их вероятность 1/p вместо одинаковой, потому меньшие простые выгоднее, они чаще делят n. На меньших интервалах, а 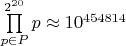 офигенно велико, распределение комбинаций остатков будет неким образом зависеть от проверяемых чисел, но будет своим для каждого интервала n (и длины и положения), плюс отличия будут малы (вот это стоит конечно проверить), плюс определить их будет не проще проверки всего интервала, КТО неплохо всё перемешивает. Т.е. зависимость будет сильнее не от паттерна (что само собой будет, но ничем не помогает в силу следующего), а от позиции и длины интервала по n внутри того офигенно огромного. Проверка какое простое сколько раз отбросило кандидата: ...
frq=vectorsmall(2^20);
for(i=0,oo,
...
x=n+#v-1;
forprime(p=59,2^20,
d=#v-x%p; if(d<1, next); nf[d]++; nn[d]*=p;
if(nf[d]>nu[d], frq[p]++;next(2));
if(x%p^2<#v, frq[p]++;next(2));
if(nf[d]==nu[d] && !ispseudoprime((n+d-1)/v[d]/nn[d],1), frq[p]++;next(2));
);
);
forprime(p=59,2^20, if(frq[p]>=100, print1(p,":",frq[p],", "));); print; 59:52292, 61:51568, 67:47241, 71:44496, 73:43001, 79:39037, 83:36610, 89:33441, 97:30072, 101:28250, 103:27163, 107:25230, 109:24368, 113:22893, 127:19761, 131:18598, 137:17390, 139:16769, 149:15038, 151:14564, 157:13608, 163:12861, 167:12187, 173:11450, 179:10913, 181:10510, 191:9547, 193:9410, 197:9002, 199:8791, 211:8026, 223:7352, 227:7031, 229:7077, 233:6797, 239:6388, 241:6288, 251:5742, 257:5447, 263:5319, 269:5059, 271:4966, 277:4610, 281:4613, 283:4583, 293:4190, 307:4152, 311:3869, 313:3723, 317:3636, 331:3385, 337:3309, 347:3138, 349:3078, 353:2944, 359:2934, 367:2740, 373:2750, 379:2609, 383:2556, 389:2454, 397:2354, 401:2399, 409:2325, 419:2158, 421:2109, 431:2129, 433:1934, 439:2035, 443:1909, 449:1870, 457:1761, 461:1789, 463:1728, 467:1743, 479:1627, 487:1582, 491:1573, 499:1490, 503:1471, 509:1457, 521:1395, 523:1456, 541:1307, 547:1298, 557:1223, 563:1184, 569:1285, 571:1150, 577:1167, 587:1132, 593:1086, 599:1148, 601:1132, 607:1028, 613:997, 617:1038, 619:1005, 631:953, 641:948, 643:933, 647:919, 653:896, 659:838, 661:890, 673:832, 677:841, 683:790, 691:839, 701:780, 709:763, 719:712, 727:741, 733:694, 739:742, 743:719, 751:621, 757:622, 761:681, 769:679, 773:604, 787:598, 797:635, 809:653, 811:562, 821:576, 823:533, 827:545, 829:546, 839:583, 853:541, 857:486, 859:532, 863:516, 877:497, 881:516, 883:543, 887:472, 907:492, 911:500, 919:449, 929:494, 937:410, 941:431, 947:441, 953:415, 967:382, 971:420, 977:403, 983:369, 991:395, 997:395, 1009:354, 1013:381, 1019:359, 1021:395, 1031:417, 1033:364, 1039:364, 1049:338, 1051:405, 1061:325, 1063:346, 1069:353, 1087:333, 1091:362, 1093:304, 1097:329, 1103:298, 1109:305, 1117:314, 1123:301, 1129:304, 1151:298, 1153:284, 1163:297, 1171:277, 1181:283, 1187:273, 1193:296, 1201:265, 1213:265, 1217:262, 1223:264, 1229:268, 1231:271, 1237:236, 1249:241, 1259:239, 1277:235, 1279:251, 1283:223, 1289:246, 1291:246, 1297:231, 1301:234, 1303:236, 1307:247, 1319:246, 1321:218, 1327:214, 1361:243, 1367:232, 1373:195, 1381:209, 1399:208, 1409:206, 1423:192, 1427:195, 1429:203, 1433:195, 1439:210, 1447:189, 1451:191, 1453:187, 1459:183, 1471:187, 1481:168, 1483:168, 1487:180, 1489:176, 1493:187, 1499:187, 1511:171, 1523:162, 1531:148, 1543:177, 1549:156, 1553:156, 1559:136, 1567:139, 1571:160, 1579:177, 1583:166, 1597:144, 1601:123, 1607:150, 1609:155, 1613:169, 1619:146, 1621:164, 1627:141, 1637:155, 1657:146, 1663:154, 1667:133, 1669:150, 1693:130, 1697:124, 1699:150, 1709:121, 1721:125, 1723:119, 1733:121, 1741:151, 1747:141, 1753:125, 1759:127, 1777:119, 1783:131, 1787:133, 1789:113, 1801:128, 1811:131, 1823:130, 1831:127, 1847:109, 1861:129, 1867:111, 1871:110, 1873:112, 1879:120, 1901:109, 1907:104, 1913:107, 1931:100, 1949:119, 1973:114, 1987:112, 2003:116, 2011:113, 2027:103, 2039:111, 2087:108, Меньше 100 раз там ещё тысячи простых, но они уже точно не интересны. Ну и всё, список простых и так уже оптимален.
|
|

 или используют её как первый шаг, а это и есть возведение длинного числа (оно сначала короткое, но по мере возведения в степень становится длинным) в степень длинного числа по модулю длинного числа, кошмар-кошмар.
или используют её как первый шаг, а это и есть возведение длинного числа (оно сначала короткое, но по мере возведения в степень становится длинным) в степень длинного числа по модулю длинного числа, кошмар-кошмар.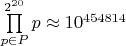 офигенно велико, распределение комбинаций остатков будет неким образом зависеть от проверяемых чисел, но будет своим для каждого интервала n (и длины и положения), плюс отличия будут малы (вот это стоит конечно проверить), плюс определить их будет не проще проверки всего интервала, КТО неплохо всё перемешивает. Т.е. зависимость будет сильнее не от паттерна (что само собой будет, но ничем не помогает в силу следующего), а от позиции и длины интервала по n внутри того офигенно огромного.
офигенно велико, распределение комбинаций остатков будет неким образом зависеть от проверяемых чисел, но будет своим для каждого интервала n (и длины и положения), плюс отличия будут малы (вот это стоит конечно проверить), плюс определить их будет не проще проверки всего интервала, КТО неплохо всё перемешивает. Т.е. зависимость будет сильнее не от паттерна (что само собой будет, но ничем не помогает в силу следующего), а от позиции и длины интервала по n внутри того офигенно огромного.