Во Вселенной остались недорешённые СЛАУ ! Помогите решить :)

[Zvezdochet]

Цитата:

Кстати, у Вас не СЛАУ вовсе

А что? А как называется?
что гуглить-то???

[Geen]

B@R5uk в сообщении #1673862 писал(а):

Не, это не задача целочисленного программирования.

Это, на самом деле, вопрос - может оказаться, что в (неназванных) условиях ТС, найти хоть какое-то "разумное" решение это единственная альтернатива полному перебору... Я вот только не совсем уверен, что минимизация суммы $y$-ков это "разумно".

[B@R5uk]

Итак, систему с ограничениями:

$$\begin{array}{c}Ax+y=b,\\ \begin{array}{ccc}A>0&\quad&b>0\\x>0&\quad&y>0\end{array}\end{array}$$

можно переписать так:

$$\begin{array}{c}0<Ax<b\\x>0\\y=b-Ax\end{array}$$

Причём в силу положительности матрицы A и столбца неизвестных x первое неравенство (с нулём) можно отбросить. Фактически, требуется посчитать число целочисленных точек, строго внутри гипергранника, ограниченного координатными гиперплоскостями (последнее неравенство на x) и гиперплоскотями, задаваемых каждой строчкой матрицы A.

-- 09.02.2025, 15:50 --

Zvezdochet в сообщении #1673811 писал(а):

Geen в сообщении #1673807 писал(а):

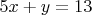
Давайте посмотрим на "уравнение" $5x+y=13$, к примеру, - сколько у него решений и какие?

Аж две штуки:
${(1;8)}$
${(2;3)}$

В данном случае задача одномерна. Требуется найти целые числа x, принадлежащие интервалу:

$$x\in\left(0,\;\frac{13}{5}\right)$$

-- 09.02.2025, 16:14 --

Первым шагом решения, пожалуй, стоит оценить количество искомых точек сверху. Величиной таковой оценки будет "объём" гиперкуба:

$$0<x<\min(b)$$

Поскольку элементы матрицы A строго положительные, в неравенстве стоит минимум. Если же они были неотрицательными (то есть могли бы равняться в том числе и нулю), то был бы максимум. Не правильно это. В случае допущения нулей, число решений может быть бесконечным.

Следующим шагом, наверное, будет перебор строчки за строчкой матрицы A и отсечение от этого гиперкуба "лишних" внутренних точек. Причём с каждой новой строчкой придётся проверять пересечение соответствующей гиперповерхности с гиперповерхностями, задаваемыми каждой из предыдущих строчек матрицы A. Может даже случится так, что очередная строчка-гиперповерхность ничего не отсекает. Или же отсекает всю "форму", которая получилась предыдущими отсечениями. Здесь напрашивается оптимизация: упорядочить строчки в порядке удаления задаваемых ими гиперповерхностей от начала координат. А так же откидывание тех строчек матрицы, соответствующие которым гиперповерхности не имеют пересечения с более "близкими" гиперповерхностями внутри целевого гиперкуба.

Возможно, конечно, что существует какой-нибудь кардинально другой подход к задаче. Я такого не знаю.

[Zvezdochet]

Спасибо огромное, буду медитировать над изложенным

[B@R5uk]

Вообще, если так подумать, то неотрицательность элементов матрицы A накладывает более жёсткие ограничения на целевой объём, содержащий искомые решения:

$$0<x_i<\overline{x_i}=\min_{j}\frac{b_j}{A_{ji}}$$

Получается прямоугольный гиперпараллелепипед. Если его целочисленных "объём"

$$V=\prod_i\bigl(\left\lceil\overline{x_i}\right\rceil-1\bigr)$$

является разумной величиной, то можно замутить брутфорс по всем точкам. Такая программа вообще от программиста практически никаких раздумий не потребует. Так что вот, ещё один вариант решения задачи (каким бы ограниченным область его применения не была).

Zvezdochet, я поправил свой пост выше, если что.

[dgwuqtj]

Zvezdochet
Проще сразу прочитать что-то про целочисленное линейное программирование (integer programming). Если нужна именно теория, а не готовый код, то можно начать с книжки Schrijver. Theory of linear and integer programming.

[B@R5uk]

dgwuqtj, я уже писал выше, что эта задача не имеет ничего общего с линейным программированием (кроме того, что есть линейная система и ограничения на переменные). В линейном программировании (будь то целочисленное или какое другое) всегда ставится вопрос оптимизации некоторой функции. Благодаря определённым условиям на задачу трудоёмкость этой оптимизации удаётся из экспоненциально сложной сделать полиномиально сложной (если мне память не изменяет). В этом вся суть программирования как задачи.

Здесь же просто объём гипертела надо посчитать. Это не имеет ничего общего с поиском вершины этого тела, на которой некая целевая функция принимает максимальное значение. Даже тот факт, что путь (по которому к этой вершине решение задачи программирования ведёт) является в некоторым смысле коротким (полиноминально длинным по количеству рёбер-шагов, а не экспоненциально длинным) тоже ничего общего с задачей ТС не имеет. Задача ТС является экспоненциально сложной и никуда от этого не деться: каждая грань на поверхности тела, "объём" которого ищется, потенциально отсекает от этого объёма искомые точки.

[Евгений Машеров]

Полагаю, в той части, где надо найти решение, исходя из того, что чем меньше шум, тем лучше, это задача ЦЛП.
А вот способа оценить число решений уравнения кроме как перебором (пусть "с отсечениями") я не вижу.

[B@R5uk]

Евгений Машеров в сообщении #1673890 писал(а):

исходя из того, что чем меньше шум, тем лучше

В условии задачи ТС этого нет. Хотя я вижу, что вы имеете в виду. Профессионалы в вопросе будут что-то подобное подразумевать по умолчанию. В то же время, отсылка ТС к линейному программированию не только заведёт его в дебри, откуда ему самому не выбраться (судя по первому посту), но и к решению поставленной им задачи не приблизит.

Другое дело было бы, если бы ТС рассказал, откуда эта задача возникла и как он её решение собирается применять.

[dgwuqtj]

Количество целых точек в выпуклом многограннике $P$ оценить через объём можно, но надо это делать аккуратно, чтобы учесть всё, что рядом с поверхностью. Например, можно взять объём суммы Минковского $P + [0, 1]^d$ в качестве верхней оценки (можно и шар прибавлять, но тогда будет не многогранник, считать сложнее).

Zvezdochet, а какие у вас размеры этой матрицы? Нам бы понимать, сойдёт ли наивный алгоритм, или нужно что-то умное/приближённое. Скажем, искать объём многогранника в $1000$-мерном пространстве, если даны $10000$ граней, уже сложно, и это без учёта прибавления гиперкуба.

B@R5uk в сообщении #1673889 писал(а):

dgwuqtj, я уже писал выше, что эта задача не имеет ничего общего с линейным программированием (кроме того, что есть линейная система и ограничения на переменные). В линейном программировании (будь то целочисленное или какое другое) всегда ставится вопрос оптимизации некоторой функции.

Это, конечно, верно, но вообще полезную теорию проще всего искать именно в литературе по целочисленному линейному программированию. Про готовые библиотеки не скажу, но думаю, что их тоже проще найти по этим ключевым словам.

[Zvezdochet]

Матрица детская совсем: 8х8
стыдно к людям выходить с такой

Коэффициенты - от десятков до нескольких тысяч.

Зато все переменные(x, noise) <= 10^10

[dgwuqtj]

Так с этого начинать и надо было! Количество точек внутри посчитать, может, и реально (с длинной арифметикой), а вот чтобы их всех найти, просто не хватит памяти.

[B@R5uk]

ОК, и я, оказывается, невнимательно условие читал. На игреки тоже есть ограничение, они заметно меньше соответствующих элементов столбца b:

$$y=b-Ax<c\sim(0.01\ldots 0.001)b$$

Это приведёт к тому, что гипергранник немного сложнее:

$$\begin{array}{c}b-c<Ax<b\\x>0\\y=b-Ax\end{array}$$

То есть он заключён между наборами параллельных гиперплоскостей, расположенных в некотором смысле "близко" друг к другу. Здесь координатые гиперплоскости всё ещё играют роль, но вероятность, что даже хотя бы одна из них (из их экспонециального количества) является поверхностью гипергранника будет значительно меньше. И объём гипергранника будет значительно меньше, если решения вообще возможны с переопределённой системой.

Было бы здорово, если бы ТС привёл какой-нибудь рабочий пример поиграться. И порядки величин были бы сразу видны, и количество переменных, и характер матрицы (читай: взаимное положение гиперплоскостей).

-- 09.02.2025, 17:41 --

Вообще, задача чем-то напоминает олимпиадные задачки с ацм-тимус-ру из раздела "с зубодробящей сложностью".

[zgemm]

А я бы пошел классическим путем.

Записал бы

$$\min_{x} ||Ax - b||_2^2 + \lambda_1 ||x||_2^2 + \lambda_2 ||[x]-x||_2^2 + \lambda_3 ||[Ax-b]-(Ax-b)||_2^2,$$

где $||.||_2^2$ - Евклидова/Фробениусова норма, и итерировал бы каким-нибудь хоть даже квази-ньютоном, стартовав с нулевых $\lambda_2$ и $\lambda_3$ и значением для $\lambda_1$ как учит Тихонов, а потом бы медленно и монотонно вгонял бы $\lambda_2$ и $\lambda_3$ в плюс бесконечность, а с $\lambda_1$ может и не трогал бы, а может немного уменьшил.

[zgemm]

а чтобы найти другие решения, в изредка дергал бы вместо квази-ньютона метод отжига, и ловил бы новое решение. Все решения, если их много, найти будет не реально, а вот найти сколько-то близких к оптимуму - будет довольно быстро сходиться.

Метод отжига в несколько строк легко самому запрограммировать. Квазиньютон есть в массе бесплатных пакетов, хотя можно тоже самому, по википедийной формуле на BFGS, или даже https://en.wikipedia.org/wiki/Limited-memory_BFGS .