Поведение жидкого самогравитирующего тела

[sergey zhukov]

Давно интересовало поведение жидкого самогравитирующего тела. Я слышал, форма Земли с высокой точностью является такой фигурой, т.е. Земля может рассматриваться в этой задаче, как жидкая. Для начала подсчитал эту задачу для "жидкого диска". Это самогравитирующий плоский жидкий диск (задача, конечно, не особо реальная, но так для начала проще считать):

На картинке следующее: взято первое приближение геометрии тела (в данном случае - квадрат, его эскиз нарисован синим в левом углу, его четверть нарисована крупнее на заднем плане с красной границей, но практически сразу он превращается в круг). Он вращается вокруг оси, перпендикулярной плоскости квадрата и проходящей через его центр. Скорость вращения медленно нарастает (указана ниже слева). Т.е. это у нас "вид сверху" вдоль оси вращения.

Расчет численный итерационный. Его цель - подобрать такую геометрию тела, чтобы линия $\varphi=const$ совпала с периметром тела (это замкнутая линия, если решение существует). Если совпадения нет, алгоритм обрезает точки тела, которые вышли за пределы контура $\varphi=const$ и добавляет точки тела внутри контура $\varphi=const$, если там получаются пустоты. Этот поиск сходится к решению, при котором контур $\varphi=const$ полностью заполнен веществом внутри и пуст вовне.

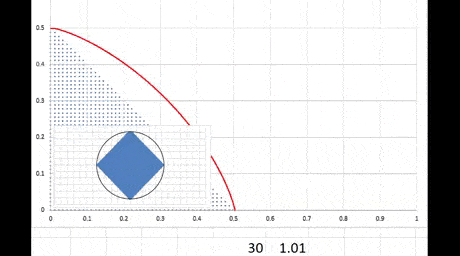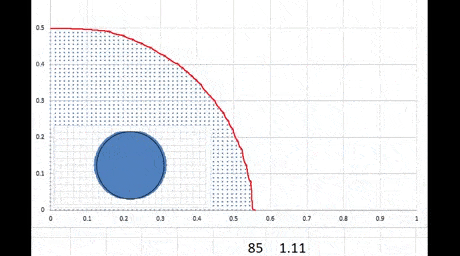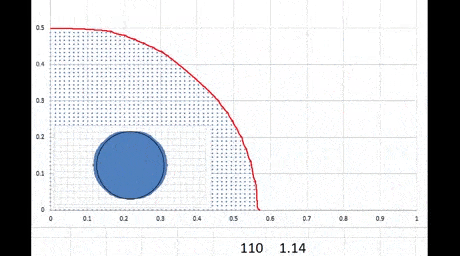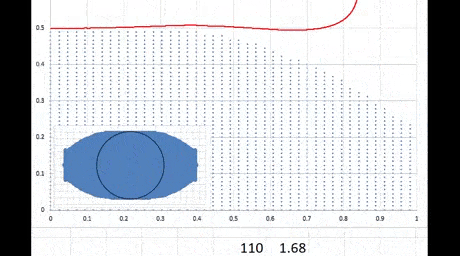
Как видно, при малых скоростях вращения форма диска представляет собой что-то вроде эллипса, только больше похожего на прямоугольник с двумя полукругами. При отношении горизонтального и вертикального размеров примерно >1.17 (отображается снизу справа, критическая скорость вращения ~ 110) решение не существует: расчет расходится, линия $\varphi=const$ (красная) разрывается и расчет несколько раз стартует заново. Т.е. не сильно такой диск можно "растянуть".

Я надеялся, что есть какое-то решение вроде гантели. Но, похоже, такого для плоского диска нет.

В этом расчете плотность диска получается падающей, а вертикальный размер - постоянный. В реальной задаче об ускорении такого диска его плотность была бы постоянной, а вертикальный размер - уменьшающимся. Эти задачи, конечно, эквивалентны, т.к. форма фигуры не зависит от плотности жидкости и размеров тела ( определяется только скоростью вращения). Тут просто вопрос масштабирования.

[DimaM]

sergey zhukov
А силу тяжести на полюсе и экваторе считаете? Интересно построить график в зависимости от угловой скорости.

[sergey zhukov]

DimaM
Это вы наверное имеете ввиду силу тяжести в точках на 12 и на 3 часа на этой картинке. Так-то это плоский диск, вид сверху, вращается в плоскости рисунка. Тут не понятно, что называть полюсом, что - экватором. Можно посчитать.

[manul91]

sergey zhukov в сообщении #1671042 писал(а):

Он вращается вокруг оси, перпендикулярной плоскости квадрата и проходящей через его центр. Скорость вращения медленно нарастает (указана ниже слева). Т.е. это у нас "вид сверху" вдоль оси вращения.

Непонятно откуда берется ассиметрия.
В плоскости картинки никаких выделенных направлений нет по условию (ось вращения перпендикулярна плоскости и проходит через центр изначального квадрата). Ассиметрия исходной фигуры не должна играть заметную роль (т.к. при вращении все направления обходятся одинаковым образом) - да и она итак довольно симметрична (квадрат). В частности непонятно почему растягивается именно горизонтально, а не например вертикально.

[DimaM]

sergey zhukov в сообщении #1671049 писал(а):

Это вы наверное имеете ввиду силу тяжести в точках на 12 и на 3 часа на этой картинке.

Именно так.

sergey zhukov в сообщении #1671049 писал(а):

Тут не понятно, что называть полюсом, что - экватором.

Полюса - точки, через которые проходит ось. Экватор - линия, равноудаленная от полюсов.

manul91 в сообщении #1671050 писал(а):

В частности непонятно почему растягивается именно горизонтально, а не например вертикально.

Насколько я понимаю, показана четверть центрального сечения. Ось ординат совпадает с осью вращения. Потому растягивается в перпендикулярном оси направлении.

[Dedekind]

DimaM

sergey zhukov в сообщении #1671049 писал(а):

плоский диск, вид сверху, вращается в плоскости рисунка

[sergey zhukov]

manul91
Вначале имеем неустойчивое равновесие. Но это же численная модель, изначально легкая несимметричность присутствует, равновесие быстро нарушается.

Расчет ведется в предположении, что форма фигуры одинакова во всех четырех квадрантах. Соответственно, потенциал считается в показанном квадранте, а в остальные он просто копируется. Поэтому оси симметрии фигуры лежат на осях координат.

Почему она вытягивается именно в горизонтальном направлении? Тут дело в том, по какой именно $\varphi=const$ мы "равняем" периметр тела на каждом шаге. В этом расчете сделано так, что это всегда та линия $\varphi=const$, которая касается периметра тела в верхней точке. Это приводит к "приросту" именно в горизонтальном направлении.

Даже если взять исходную конфигурацию, вытянутую вверх, все равно она тут будет расти горизонтально. Это же не решение задачи динамики диска.

-- 22.01.2025, 12:29 --

DimaM
Не, тут ось проходит через центр картинки. Перпендикулярно ей. Это мы смотрим вдоль оси вращения.

[DimaM]

sergey zhukov в сообщении #1671056 писал(а):

Не, тут ось проходит через центр картинки. Перпендикулярно ей. Это мы смотрим вдоль оси вращения.

Гм, тогда смысл сей симуляции от меня ускользает.
Разумно решать осесимметричную задачу.

[sergey zhukov]

DimaM
Да уж решил, что мог. Для начала. Можно, впрочем, этот диск попробовать покрутить вокруг диаметра. Это даже проще.

[Geen]

sergey zhukov в сообщении #1671061 писал(а):

Да уж решил, что мог.

Напишите, пожалуйста, уравнения, которые Вы решали.

[sergey zhukov]

Geen

Да что тут писать? Взял любое начальное приближение тела, нашел вокруг него произвольную замкнутую $\varphi=const$ ($\varphi$ - сумма гравитационного и центробежного потенциалов) такую, чтоб где-нибудь она пересекала или касалась границы тела. На следующем шаге взял эту $\varphi=const$ за новую границу тела и т.д.

Как считать потенциалы, я думаю, тут пояснять не нужно.

[Geen]

sergey zhukov в сообщении #1671079 писал(а):

такую, чтоб где-нибудь она пересекала или касалась границы тела. На следующем шаге взял эту $\varphi=const$ за новую границу тела

Я правильно понимаю, что масса не сохраняется?

[sergey zhukov]

Geen
Нет, масса тут сохраняется, но плотность - нет (потому, что плащадь фигуры увеличивается). Плотность падает.

Число расчетных ячеек фиксированной массы внутри тела постоянно, они равномерно распределяются по телу в процессе его растяжения. Т.е. я тут не слежу за условием постоянной площади тела и постоянной плотности материала. Это не органичивает общности решения, все равно оно зависит (с точностью до масштаба) только от скорости вращения.

[Geen]

sergey zhukov в сообщении #1671096 писал(а):

с точностью до масштаба

А "масштаб" чем определяется?

[sergey zhukov]

Geen
Я имею ввиду, что независимо от плотности жидкости, размеров тела, гравитационной постоянной форма тела зависит только от угловой скорости вращения. Поэтому вообще все равно, что в процессе решения с расстояниями, плотностью, площадью, массой и величиной гравитационного потенциала происходит.

В частности, в этом расчете я зафиксировал только координаты точки пересечения/касания периметра тела и линии $\varphi=const$ в точке (0;0,5). Все остальное само получается. В частности, вертикальный размер тела получается всегда равным 0,5.