Делители нуля в кольце остатков в поле из 4х элементов.

[seraphimt]

Добрый день. Подскажите, пожалуйста с таким вопросом: найти все делители нуля и все обратимые в кольце$\mathbb F_4/(x^2+[\alpha]x+1) $, где $\mathbb F_4$ - поле из 4х элементов $\{1, x, [\alpha], [\alpha+1]\}$.
Я рассуждал так: возьмём два элемента $(ax+b)$ и $(cx+d)$ из кольца, перемножим и посмотрим, когда остаток от деления результата на (x^2+[\alpha]x+1) $ будет 0 (или 1 для обратимых).
В итоге получил систему с элементами из $\mathbb F_4$:
$\begin{cases} ac+bd=0 \\ ad+bc+[\alpha]ac=0 \end{cases}$
Но на этом шаге застопорился, непонятно как отсюда выразить, кроме прямого перебора.

[KhAl]

seraphimt писал(а):

где $\mathbb F_4$ - поле из 4х элементов $\{1, x, [\alpha], [\alpha+1]\}$.

Поле — это множество с заданными на нём операциями $+$, $\cdot$, нулём и единицей. Что такое $0$ и как устроено сложение и умножение в вашем множестве $\{1, x, [\alpha], [\alpha+1]\}$?

[seraphimt]

KhAl
Да, опечатался, там вместо $x$ 0.

[dgwuqtj]

Вы можете найти корни многочлена $x^2 + [\alpha] x + 1$ в $\mathbb F_4$?

[KhAl]

seraphimt писал(а):

Да, опечатался, там вместо $x$ 0.

и вместо $\mathbb F_4/(x^2+[\alpha]x+1)$ там $\mathbb{F}_4[x]/(x^2+[\alpha]x+1)$

[seraphimt]

dgwuqtj в сообщении #1616538 писал(а):

Вы можете найти корни многочлена $x^2 + [\alpha] x + 1$ в $\mathbb F_4$?

Да, действительно, о таком не подумал. Значит нет таких остатков, что дали бы ноль, кроме нулевых.
Насчёт обратимых у меня вышло так. Для констант очевидно есть обратимый, для выражений вида $ax$ тоже и равняется $(a^{-1}x+[\alpha]a^{-1})$
Остался случай, когда оба коэффициента не ноль, тогда используя систему, что приводил выше, можно получить:
$d=(\alpha+ba^{-1})(a+b^2a^{-1}+\alpha b)^{-1}$
$c=(1+bd)a^{-1}$
Отсюда условия на обратимость: $(a+b^2a^{-1}+\alpha b) \ne 0$ и $(\alpha+ba^{-1}) \ne 0 $. Первое выполнено всегда(перебрал все 9 случаев), второе верно при $b\ne \alpha a$

[dgwuqtj]

Мне что-то подсказывает, что там вообще получится поле. Зачем вам обратимость именно $d$?

[seraphimt]

dgwuqtj в сообщении #1616558 писал(а):

Зачем вам обратимость именно $d$?

Это условие не только на него, но и в целом. Туда нужно включить $1+bd \ne 0$ ещё, да. Потому что если $c$ или $d$ будут нуль, то это будет другой случай, который разбирался выше.

[dgwuqtj]

Может, я не уследил за всеми случаями, но у вас счала разбираются $a = 0$ и $b = 0$, а потом в общем случае почему-то вдруг $c$ и $d$ ненулевые.

[seraphimt]

dgwuqtj в сообщении #1616562 писал(а):

Может, я не уследил за всеми случаями, но у вас счала разбираются $a = 0$ и $b = 0$, а потом в общем случае почему-то вдруг $c$ и $d$ ненулевые.

Потому, что если они нулевые, то мы по сути опять рассматриваем случай с $a = 0$ или $b=0$ из-за симметричности $(ax+b)(cx+d)=1$

[StepV]

KhAl в сообщении # писал(а):

возьмём два элемента $(ax+b)$ и $(cx+d)$ из кольца, перемножим и посмотрим

До перемножения элементов кольца надо иметь таблицы умножения и сложения в этом факторкольце. Сделайте следующее:
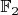
1. Сначала нужны таблицы умножения и сложения для поля. Как я понимаю, для этого поля существует два варианта таблиц, в зависимости от того, какой из двух многочленов второй степени, неразложимых в $\mathbb{F}_2$, взят.
2. Используя эти таблицы проверить, является ли заданный многочлен неразложимым в данном поле. Если он не разложим, то факторкольцо является полем и: нет делителей нуля, все элементы обратимые. Если он разложим в поле, то переходим к п.3.
3. Расчитать таблицу умножения и сложения для вашего факторкольца. Она состоит из $4^2$ элементов.
Когда таблица получена, по ней легко определяются обратимые и делители нуля. Упражнение в перемножении двух абстрактных элементов поля отпадает.

[dgwuqtj]

Разве что над $\mathbb F_2$ есть только один неприводимый многочлен 2 степени.

[StepV]

dgwuqtj в сообщении #1616599 писал(а):

Разве что над $\mathbb F_2$ есть только один неприводимый многочлен 2 степени.

Спасибо! В уме разложил $x^2+1$ и ошибся .

[seraphimt]

StepV в сообщении #1616598 писал(а):

о факторкольцо является полем и: нет делителей нуля, все элементы обратимые.

Делители нуля понятно, а откуда следует, что если неразложим - то есть обратные для всех?

[dgwuqtj]

Это стандартный результат из теории полей, если $f \in F[x]$ неприводим и $F$ поле, то $F[x] / (f)$ тоже является полем. Похоже, вам придётся это в лоб доказывать в частном случае.