Регрессия квадратичного полинома

[ValDec]

Помогите получить формулы вычисления коэффициентов параболической регрессии
без использования матриц.

[Александрович]

Систему трёх уравнений с тремя неизвестными сможете решить?

[ValDec]

Речь идет о массиве 500...1000 точек и аппроксимации их параболой.

[Александрович]

ValDec

Александрович в сообщении #1590729 писал(а):

Систему трёх уравнений с тремя неизвестными сможете решить?

[Alex-Yu]

Александрович в сообщении #1590729 писал(а):

Систему трёх уравнений с тремя неизвестными сможете решить?

Причем линейных уравнений.

Ну а по существу заданного вопроса... Запишите в общем виде ("в буквах") сумму квадратов отклонений от параболы, продифференцируйте эту сумму по коэффициентам параболы (чтобы минимум найти) и приравняйте эти производные нулю. Получите СЛАУ на 3 переменные. Помнится, в мое время такие СЛАУ школьники решали.

[LLeonid3]

Alex-Yu в сообщении #1590749 писал(а):

Помнится, в мое время такие СЛАУ школьники решали

Это точно!

Alex-Yu в сообщении #1590749 писал(а):

Запишите в общем виде ("в буквах") сумму квадратов отклонений от параболы

А вот это тяжело при тысяче точек
Для каждой точки необходимо провести перпендикуляр к искомой параболе (это не сложно), найти точку пересечения перпендикуляра и параболы, а это посложнее, формула получается длинная и имеет пару решений, как выбрать подходящее "в буквах" не очень понятно, искомые коэффициенты параболы в степенях от куба, да и после суммирования и дифференцирования получится не простенькая СЛАУ
Легче подгоном на компьютере выполнить

[Alex-Yu]

LLeonid3 в сообщении #1590786 писал(а):

А вот это тяжело при тысяче точек

Ничего не сложно. И не надо никаких перпендикуляров. Пусть ваша аппроксимирующая парабола это $y=f(x)=ax^2+bx+c$. Пусть ваши точки это $x_i,y_i$. Минимизируйте (беря производные по $a,b,c$ и приравнивая их нулю) сумму таких величин: $(y_i-f(x_i))^2$. Очень простая задача.

[LLeonid3]

Alex-Yu в сообщении #1590749 писал(а):

сумму квадратов отклонений от параболы

Отклонение по Y не есть минимальное расстояние от точки до функции, соответственно такое упрощённое решение не будет оптимальным, хотя, конечно, имеет право на применение

[пианист]

LLeonid3 в сообщении #1590816 писал(а):

Отклонение по Y не есть минимальное расстояние от точки до функции

Видимо, до графика.
А откуда взялась данная оптимальность, и зачем она нужна?

[GAA]

пианист в сообщении #1590819 писал(а):

А откуда взялась данная оптимальность, и зачем она нужна?

В начальном сообщении темы ничего не сказано о модели. Отклонения ищутся по ординате (в случае полиномиальной зависимости $y$ от $x$) в предположении, что погрешности имеют только измерения $y$, а $x$ измеряются точно. Грубо говоря, если модель имеет вид

$y_i = ax_i^2+ bx_i+cx_i + \varepsilon_i,$

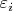
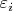
где $\varepsilon_i$ — независимые и одинаково распределённые случайные величины с нулевым математическим ожиданием. Тогда будет справедлива теорема Гаусса — Маркова. А если предположить и нормальность $\varepsilon_i$, то возможно построить доверительные интервалы для параметров и критерии проверки гипотез.
Или Вы не об этом спрашиваете?

[пианист]

GAA
Я так же считаю, когда требуется, но, честно говоря, без глубокого погружения в предмет :).
Но выше высказано утверждение (если я правильно понял), что это а) упрощенный вариант, б) надо минимизировать не сумму квадратов отклонений ординат, а сумму расстояний (или квадратов расстояний?) до графика.
Вот и интересно, когда и почему так лучше.

[Alex-Yu]

LLeonid3 в сообщении #1590816 писал(а):

такое упрощённое решение не будет оптимальным,

Никто "оптимально" в вашем смысле не делает. И регрессией это не называет. Регрессия -- это именно так, как я сказал.

-- Пн апр 24, 2023 00:24:20 --

GAA в сообщении #1590823 писал(а):

$y_i = ax_i^2+ bx_i+cx_i + \varepsilon_i,$

Здесь, видимо, опечатка: нет никакого смысла писать линейный член дважды.

[sergey zhukov]

LLeonid3 в сообщении #1590786 писал(а):

Для каждой точки необходимо провести перпендикуляр к искомой параболе

Я в школе тоже думал, что это лучшее решение. Только на самом деле это вообще чушь. Например, перпендикуляр из точки на кривую зависит от масштабов по осям, в которых построен график, чего явно быть не должно. Скажем, умножив масштаб по $x$ вдвое, мы делаем все наши перпендикуляры не перпендикулярными, и их нужно строить заново.

[Dedekind]

sergey zhukov в сообщении #1590827 писал(а):

Например, перпендикуляр из точки на кривую зависит от масштабов по осям, в которых построен график, чего явно быть не должно.

Ну, можно же нормировать данные, это не проблема. А еще есть соображения, почему чушь?

[sergey zhukov]

Dedekind
Если у вас по $x$ метры, а по $y$ - килограммы, то что тут можно нормировать? Вообще, "длина перпендикуляра" в этом случае не имеет смысла, как сумма килограммов с метрами.

Если по обеим осям переменные одной размерности (скажем, нарисована орбита тела, т.е. по $x$ и $y$ отложены метры) - тогда еще имеет смысл рисовать эллипс и вычислять длину перпендикуляра от точек до эллипса. Такая длина просто хотя бы будет иметь смысл. То, что именно она должна быть мерилом отклонения - это еще вопрос.