Космологическая модель Эдварда Милна

[sergey zhukov]

Пока разбирался в космологии Фридмана, еще раз столкнулся с космологической моделью Эдварда Милна. Почему-то ее редко упоминают в научно-популярной литературе, хотя, по моему, это было бы очень полезно. Вообще очень полезно, как мне кажется, разбирать неправильные, но интуитивно понятные и устоявшиеся представления для того, чтобы выявить их несостоятельность. Кроме того, это отличный пример относительности различных понятий (их зависимости от выбранной системы координат).

Правильно ли я понимаю, что:

1. Модель Милна – это строгое решение уравнения Эйнштейна, частный случай открытой фридмановской модели, в которой плотность материи не просто меньше критической, а вообще устремлена к нулю. Соответственно, пространство-время такой вселенной является плоским. Поскольку пространство-время здесь плоское, можно обойтись без ОТО и криволинейных координат и использовать только СТО и простые “прямолинейные” координаты. Метрика простанства-времени здесь статическая, поэтому никакого расширения пространства не происходит;

2. Модель Милна представляет вселенную именно так, как ее представляет большинство людей, впервые услышавших о Большом взрыве (как взрыв и последующий разлет облака осколков в пустом пространстве). Небольшая сложность состоит в том, что этот взрыв следует рассматривать в рамках СТО, а не ньютоновской механики:



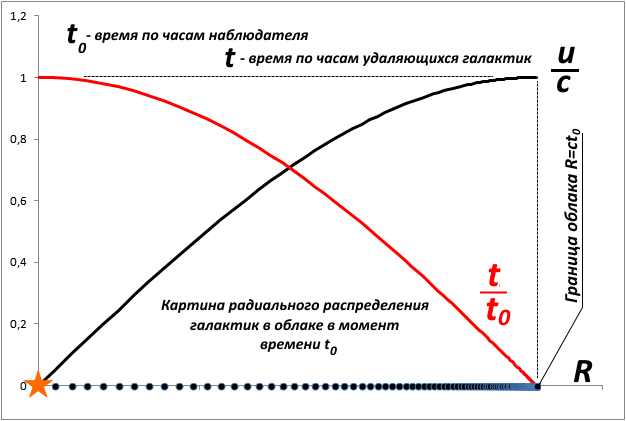
3. Вселенная Милна, как сферическое облако осколков, в каждый момент времени имеет конечный размер и расширяется со скоростью света в пустоту. За пределами облака во вселенной Милна просто бесконечная пустота;

4. Поскольку плотность материи в облаке бесконечно мала, все осколки (галактики) в такой вселенной гравитационно не взаимодействуют и имеют постоянную во времени скорость разлета;

5. Красное смещение в модели Милна объяснется именно обыкновенным (релятивистским) Доплер-эффектом, а не расширением пространства;

6. Во вселенной Милна в облаке конечного размера помещается бесконечное количество осколков-галактик. Это объяснется тем, что в областях, близких к поверхности облака, объекты движутся с субстветовыми скоростями, радиальный размер объектов стремится к нулю, и поместить там любое (даже бесконечное) количество объектов оказывается возможным;

7. Модель Милна изотропная и однородная. Центр взрыва не является выделенной точкой, т.к. любая точка в облаке, если правильно применять преобразования Лоренца для перехода от системы одной галактики к системе другой, оказывается точно в таком же положении. Если в любое время $t$ (по собственным часам) наблюдатель в любой галактике измерит расстояние до края облака, то он получит, что:

a. Находится в центре облака;
b. Текущий радиус облака равен $ct$.

8. В системе любых произвольно выбранных часов любой галактики часы всех остальных (удаляющихся) галактик идут медленнее (замедление времени движущихся часов), а на границе облака они стоят. Можно сказать, что модель Милна – это модель с плоским статическим пространством-временем, в котором система координат выбрана так, что пространство оказывается плоским, но гиперповерхности $t=const$ выбраны так, что часы всех галактик показывают на них разное время. Бесконечное число галактик собрано в сфере конечного объема.
Наоборот, в соответствующем пределе модели Фридмана (с исчезающее малой плотностью материи) система координат выбрана так, что метрика пространства-времени динамическая, пространство расширяется и отрицательно искривлено, зато гиперповерхности одновременности $t=const$ выбраны так, что часы всех галактик показывают на них одно и то же время. Бесконечное число галактик заполняет пространство бесконечного объема.
При этом речь идет об одном и том же пространстве-времени, но в разных системах координат;

9. С течением времени плотность материи в открытом решении Фридмана (без $\lambda$-члена) уменьшается, поэтому открытое решение Фридмана с течением времени приближается к модели Милна;

10. Модель Милна не соответствует нашей вселенной, т.к. плотность материи в нашей вселенной (в настоящее время) никак не близка к нулю, а до этого, следовательно, была еще выше. Совпадение двух совершенно разных подходов (ОТО и СТО) в этом случае получается именно потому, что можно пренебречь гравитацией. Вся разница в описании оказывается в этом случае обязанной только разным системам координат.
Общий случай для произвольной плотности материи невозможно описывать без динамической метрики пространства, т.е. без представления о расширяющемся/сжимающемся пространстве. Поэтому подход в рамках СТО работает только в частном случае пренебрежимо малой плотности, а подход в рамках ОТО - во всех случаях.

[Geen]

sergey zhukov в сообщении #1575639 писал(а):

Вселенная Милна, как сферическое облако осколков

Не сфера.

-- 30.12.2022, 23:47 --

sergey zhukov в сообщении #1575639 писал(а):

Модель Милна не соответствует нашей вселенной, т.к. плотность материи в нашей вселенной (в настоящее время) никак не близка к нулю

Более существены, и теоретически и экспериментально, другие соображения.

-- 30.12.2022, 23:50 --

Модель де Ситтера более интересна (имхо).

[Утундрий]

sergey zhukov в сообщении #1575639 писал(а):

очень полезно, как мне кажется, разбирать неправильные, но интуитивно понятные и устоявшиеся представления для того, чтобы выявить их несостоятельность.

Крайне палеонтологический подход. Дело вкуса, конечно. Нравится ковыряться, ковыряйтесь. Только нужны, наверное, какие-то инструменты. Оно зачастую окаменелое.

[sergey zhukov]

Geen
Не сфера, а шар, конечно.

Вот здесь есть пример метрики пространства де Ситтера. Сказано, что она может быть получена из метрики Фридмана, если рассматривать решение для экспоненциально расширяющейся вселенной, т.е. $\lambda>0$ и $\rho\to0$ (функция масштабного фактора будет $a(t)=a_0e^{\sqrt{\frac{\lambda}{3}}t}$). Далее для простоты я взял $a(t)=e^t$.

Допустим, мы имеем метрику пространства де Ситтера (т.е. метрика в статических координатах), как она приведена в этой книжке:

$$ds^2=(1-r^2)d\tau^2-r^2d\Omega^2-\frac{1}{1-r^2}dr^2$$

И хотим перейти от нее к метрике Фридмана, в которую подставлено $a(t)=e^t$, т.е.:

$$ds^2=dt^2-(e^tF(\chi))^2d\Omega^2-(e^t)^2d\chi^2)$$

Формулы преобразования координат не приведены. Но из сопоставления метрик сразу можно заметить, что должно быть:

$$r=e^tF(\chi)$$

Если подставить это в метрику де Ситтера, то можно найти, что для $\tau$ должно быть:

$$\tau=-\frac{1}{2}\ln(e^{-2t}-F(\chi)^2)$$

Если применить эти формулы перехода, то результат будет такой:

$$ds^2=dt^2-(e^tF(\chi))^2d\Omega^2-(e^tF(\chi)^\prime)^2d\chi^2)$$

При $d\chi^2$ есть лишний квадрат производной $F(\chi)^\prime$. Правильно ли я понимаю, что в данном случае нужно положить $F(\chi)=\chi$ и $F(\chi)^\prime=1$, как это должно быть для плоской вселенной?

Я правильно понимаю, что при достаточно большом $\lambda$ все три решения Фридмана независимо от начальной плотности/кривизны и замкнутости/открытости становятся бесконечными во времени и асимптотически выходят на экспоненциальное расширение пустого пространства, а их радиус кривизны стремится к бесконечности? Т.е. все они стремятся к одному и тому же пределу (вакуумное решение для экспоненциально расширяющегося плоского пространства). Этот предел (в статических координатах) и описывает решение де Ситтера. Поэтому мы и должны положить $F(\chi)=\chi$. Так? Или я просто ошибся в формулах преобразования?

[Утундрий]

sergey zhukov в сообщении #1576132 писал(а):

пример метрики пространства де Ситтера. Сказано, что она может быть получена из метрики Фридмана, если

...последняя перестанет быть метрикой Фридмана?

[sergey zhukov]

Утундрий
Не перестанет. Правильнее говорить, конечно "пространство де Ситтера в координатах де Ситтера (любых статических координатах) или в координатах Фридмана".

Скобку случайно лишнюю после $d\chi^2$' поставил в двух местах, кстати.