Задача о назначениях. Как решать?

[B@R5uk]

Постановка классическая: есть таблица N на N чисел. Необходимо выбрать N чисел так, чтобы на каждом столбце и в каждой строке было ровно по одному выбранному числу, а их сумма была минимальна.

Решение в лоб — перебор всех N! вариантов с выбором оптимального — разумным назвать нельзя.

Разумеется, первым алгоритмом решения этой задачи, который попался на глаза, был Венгерский алгоритм. Википедия упоминает некий Алгоритм аукциона, который оказался распределённым алгоритмом (для параллельного программирования, другими словами) и меня не интересует, и более универсальный симплекс-метод, с которым я не знаком, и поэтому, даже понятия не имею как его можно прикрутить к интересующей меня задаче.

Венгерский алгоритм я нашёл в книге Кристофидес - Теория Графов. Алгоритмический подход и Таха - Введение в исследование операций. В первой книге два варианта: через теорию графов и матричный подход. Первый подразумевает освоение всего предыдущего материала (а приводится он в конце книги), а в объяснении тонкостей матричного подхода делаются аналогии с методом графов, что тоже улучшению моего понимания не способствует. В книге Таха дано подробное описание метода решения, и сам алгоритм решения кажется понятным. Однако, даже если забыть про то, что алгоритм предназначен для ручного счёта, остаётся несколько вопросов: зачем нужно то действие и почему это вообще работает? В частности, следующее.

В случае, когда после вычитания минимальных элементов в строках и столбцах оптимальное назначение найти не удалось, то производится некая процедура вычёркивания строк и столбцов, после чего среди не вычеркнутых ищется минимальный элемент, вычитается из всех не вычеркнутых и (ВНИМАНИЕ!) прибавляется к элементам стоящим на пересечении вычеркнутых сток и столбцов. Вопрос: зачем, ведь они всё равно не используются?

Так же меня постоянно напрягают слова "если оптимальное назначение существует". Другими словами, если существует такой выбор элементов матрицы, что каждый выбранный элемент является единственным в своих строке и столбце, а так же является нулём, то это оптимальное решение. Когда человек решает задачу, то ему такие комбинации при вдумчивом вглядывании в таблицу стразу бросаются в глаза. Но если задачу решает компьютер, то мы возвращаемся к самому началу: перебору N! вариантов, которое облегчается отсеиванием ненулевых элементов. Это при условии, что нулевых элементов мало. А если много и матрица достаточно велика? Перебирать даже $(N/4)^{N/4}$ вариантов весьма неприятно при больших N. Существует ли какой-либо более разумных способ алгоритмизации слов "оптимальное назначение существует"?

Существует ли какие-нибудь другие алгоритмы? Например в этой теме некий участник Zealint утверждает, что ему такие известны. Однако на сайте, куда он ссылается, я не нашёл ничего содержательного. Может быть кто-то ещё занимался подобными вопросами и знает решение?

Например, будет ли такой жадный алгоритм давать оптимальное решение?
1) находим в таблице минимальный элемент и запоминаем его.
2) вычёркиваем строку и столбец его содержащие
3) если в таблице остался только один элемент, то он является последним искомым и алгоритм заканчивается. В противном случае с оставшейся таблицей переходим к пункту 1)

Буду очень благодарен любой помощи.

[mihaild]

B@R5uk в сообщении #1271904 писал(а):

Вопрос: зачем, ведь они всё равно не используются?

Они используются дальше. Т.е. строки и столбцы не "вычеркиваются" до конца алгоритма, а просто выбирается минимальное их число так, чтобы покрыть все нули. Дальше выбранные строки продолжают участвовать в алгоритме на "общих правах".

B@R5uk в сообщении #1271904 писал(а):

Существует ли какой-либо более разумных способ алгоритмизации слов "оптимальное назначение существует"?

Это называется максимальным паросочетанием в двудольном графе.

B@R5uk в сообщении #1271904 писал(а):

Например, будет ли такой жадный алгоритм давать оптимальное решение?

Нет. Если $A$ может сделать работу 1 за $0$, работу 2 за $1$; $B$ может сделать работу 1 за $1$, работу 2 за $100500$, то ваш алгоритм выдаст решение стоимостью $100500$ вместо $2$.

[B@R5uk]

mihaild в сообщении #1271917 писал(а):

Нет.

Спасибо. Простой и наглядный контрпример.

mihaild в сообщении #1271917 писал(а):

Они используются дальше.

Я, кажется, понял в чём была моя проблема. Те прочитанные мною примеры, на которых разбирался алгоритм, содержали на пересечении не нулевые элементы, поэтому добавление к ним ещё чего-то погоды не делало. Если же, как например в вашем контрпримере, на пересечении будет ноль, то к нему добавится число, в результате эти строка и столбец могут вновь подвергнуться измерениям на этапах вычитания минимального элемента. Жаль, что такой важный момент нигде не уточняется.

mihaild в сообщении #1271917 писал(а):

Это называется максимальным паросочетанием в двудольном графе.

То есть компьютерная реализация Венгерского алгоритма так или иначе обращается к теории графов и обойти это нельзя?

А есть ли какие-нибудь альтернативные, качественно другие алгоритмы? Вон, пользователь Zealint утверждает, что Венгерский алгоритм далеко не самый быстрый. Стоит ли ему верить?

[B@R5uk]

Добрые люди подсказали мне грамотное изложение Венгерского алгоритма с вариантом его реализации за время $O(N^3)$. При чтении текста сразу чувствуется, что автор понимает, что пишет (чего не скажешь об авторах статей в википедии). Разъяснение толковое, вариант кода рабочий. Я уже даже перевёл его на Java.

Собственно алгоритм (файл HungarianAlgorithm.java):

(Оффтоп)

import java.util.*;

public class HungarianAlgorithm {
   public static int getAssignment(int[][] a, int[] ans) {
      int n, m, h, w, n0, m0, m1, delta, cur;
      int[] u, v, p, way, minv;
      boolean[] used;
      h = 1 + a.length;
      w = 1 + a[0].length;
      if (h > w) {
         throw new IllegalArgumentException("Data height must be less than or equal data width.");
      }
      u = new int[h];
      v = new int[w];
      p = new int[w];
      way = new int[w];
      minv = new int[w];
      used = new boolean[w];
      for (n = 1; h > n; n++) {
         p[0] = n;
         m0 = 0;
         Arrays.fill(minv, Integer.MAX_VALUE);
         Arrays.fill(used, false);
         do {
            used[m0] = true;
            n0 = p[m0];
            delta = Integer.MAX_VALUE;
            m1 = 0;
            for (m = 1; w > m; m++) {
               if (!used[m]) {
                  cur = a[n0 - 1][m - 1] - u[n0] - v[m];
                  if (minv[m] > cur) {
                     minv[m] = cur;
                     way[m] = m0;
                  }
                  if (delta > minv[m]) {
                     delta = minv[m];
                     m1 = m;
                  }
               }
            }
            for (m = 0; w > m; m++) {
               if (used[m]) {
                  u[p[m]] += delta;
                  v[m] -= delta;
               } else {
                  minv[m] -= delta;
               }
            }
            m0 = m1;
         } while (0 != p[m0]);
         do {
            m1 = way[m0];
            p[m0] = p[m1];
            m0 = m1;
         } while (0 != m0);
      }
      if (null != ans) {
         for (n = 1; w > n; n++) {
            n0 = p[n];
            if (0 != n0) {
               ans[p[n] - 1] = n - 1;
            }
         }
      }
      return -v[0];
   }
}

Оболочка для тестирования (файл StudyHungarian.java):

(Оффтоп)

import java.util.*;

public class StudyHungarian {
   private static final Random rng = new Random();
   private static final int maxRand = 24;
   private static final int width = 8;
   private static final int height = 6;
   private static final int[][] data = new int[height][width];
   public static void main(String[] args) {
      int n, m;
      for (n = 0; height > n; n++) {
         for (m = 0; width > m; m++) {
            data[n][m] = rng.nextInt(maxRand);
         }
      }
      int[] arr = new int[height];
      //=====================================================
      int res = HungarianAlgorithm.getAssignment(data, arr);
      //=====================================================
      System.out.println("The Assignment problem solution with the Hungarian algorithm:");
      for (n = 0; height > n; n++) {
         for (m = 0; width > m; m++) {
            if (arr[n] == m) {
               System.out.printf(" [%2d]", data[n][m]);
            } else {
               System.out.printf("  %2d ", data[n][m]);
            }
         }
         System.out.println();
      }
      System.out.println();
      System.out.println("Result: " + res);
   }
}

В отличие от программы в статье, для входных и выходных данных я использую индексацию от нуля. В связи с этим небольшие коррективы индексов. Так же добавил проверку размера исходной матрицы, так как алгоритм зависает, если высота больше ширины. Результат работы что-то типа этого:

The Assignment problem solution with the Hungarian algorithm:
    9  [11]  19   12    2   11    7   14 
   16   11   22   14  [ 0]  17   16   14 
   12   16   16   17    4   21  [ 4]  19 
   17    7   19   23    1  [ 2]   8   23 
  [ 4]  15   19   11   21   12   22   17 
   20   11  [12]  21    8   10   13   13 

Result: 33

Не смотря на то, что всё работает, я, к сожалению, так до конца ещё не разобрался с самим алгоритмом. То есть, я не смогу сесть и с нуля сам его написать. Однако, как любил говорить один плохой лектор по матану (он всех студентов считал дураками), лекции которого мне довелось посещать некоторое время, "Ваше дело зазубрить. Понимание придёт потом. Может быть."

mihaild, ещё раз спасибо за уделённое вами внимание. Эта задача для меня, можно сказать, решена.

[B@R5uk]

B@R5uk в сообщении #1272053 писал(а):

я, к сожалению, так до конца ещё не разобрался с самим алгоритмом.

В очередной раз штурмую неприступную крепость понимания этого алгоритма. Есть определённые подвижки: понятно, что это за потенциалы в алгоритме, как они связаны с паросочетаниями в двудольном графе, как это всё меняется в процессе работы программы. Для облегчения вникания в суть дела написал визуализацию этапов этой самой работы: как алгоритм по одной добавляет в решение строки и находит новое оптимальное назначение на основе предыдущего.

В очередной раз переписал венгерский алгоритм от Андрея Лопатина с И-Макса для индексации массива весов от нуля. В этот раз кардинально, а не просто "-1" добавил. Никаких дополнительных проверок, как там пишут, не потребовалось: просто фиктивный столбец имеет не с нулевой индекс, а — последний, а фиктивная строка вообще не нужна. За одно дал всем участвующим в работе переменным осмысленные человеческие названия:

Используется синтаксис Java

import java.util.*;

public class Study_Hungarian_2 {
    
    private static final Random rng = new Random ();

    private static int [] [] weights;
    private static int width, height;
    private static int rowIndex, columnIndex;
    private static int currentColumn, matchingRow, nextColumn;
    private static int value, delta, iterationsCount;
    private static int [] matchings, auxMinima, wayBack;
    private static int [] rowsPotential, columnsPotential;
    private static boolean [] usedColumns;
    
    public static void main(String[] args) {
        weights = getRandomTest (5, 4, 20);
//        weights = getMultiplicativeTest (8, 8);
        getAssignment ();
    }
    
    private static int [] [] getRandomTest (int width, int height, int maxValue) {
        int k, l;
        int [] [] result;
        
        result = new int [height] [width];
        for (k = 0; height > k; ++k) {
            for (l = 0; width > l; ++l) {
                result [k] [l] = rng .nextInt (maxValue);
            }
        }
        return result;
    }
    
    private static int [] [] getMultiplicativeTest (int width, int height) {
        int k, l;
        int [] [] result;
        
        result = new int [height] [width];
        for (k = 0; height > k; ++k) {
            for (l = 0; width > l; ++l) {
                result [k] [l] = (1 + k) * (1 + l);
            }
        }
        return result;
    }
    
    private static void getAssignment () {
        width            = weights [0] .length;
        height           = weights     .length;
        if (height > width) {
            throw new IllegalArgumentException ("Data height must be less than or equal data width.");
        }
        rowIndex         = -1;
        columnIndex      = -1;
        currentColumn    = -1;
        matchingRow      = -1;
        nextColumn       = -1;
        rowsPotential    = new int     [height];
        columnsPotential = new int     [width + 1];
        usedColumns      = new boolean [width + 1];
        matchings        = new int     [width + 1];
        auxMinima        = new int     [width];
        wayBack          = new int     [width];
        Arrays .fill (matchings, -1);
        
        iterationsCount = 0;
        for (rowIndex = 0; height > rowIndex; ++rowIndex) {
            //      Column with index {width} is fictitious
            matchings [width] = rowIndex;
            currentColumn = width;
            
            Arrays .fill (auxMinima, Integer .MAX_VALUE);
            Arrays .fill (usedColumns, false);
            
            //      Looking for free column
            do {
                ++iterationsCount;
                
                usedColumns             [currentColumn] = true;
                matchingRow = matchings [currentColumn];
                delta = Integer .MAX_VALUE;
                
                //      Searching current matching row for the best next column
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = weights        [matchingRow] [columnIndex] -
                            (rowsPotential [matchingRow] +
                             columnsPotential            [columnIndex]);
                    if (auxMinima [columnIndex] > value) {
                        auxMinima [columnIndex] = value;
                        wayBack   [columnIndex] = currentColumn;
                    }
                    if (delta > auxMinima [columnIndex]) {
                        delta = auxMinima [columnIndex];
                        nextColumn =       columnIndex;
                    }
                }
                
                display ();
                System .out .println ("Delta: " + delta);
                
                //      Recalculating potentials and auxiliary minima
                for (columnIndex = 0; width >= columnIndex; ++columnIndex) {
                    if (usedColumns              [columnIndex]) {
                        rowsPotential [matchings [columnIndex]] += delta;
                        columnsPotential         [columnIndex]  -= delta;
                    } else {
                        auxMinima                [columnIndex]  -= delta;
                    }
                }
                currentColumn = nextColumn;
                
                display ();
                
            } while (-1 != matchings [currentColumn]);
            
            //      Free column has been found, restoring new assignment using wayBack
            do {
                nextColumn = wayBack [currentColumn];
                matchings [currentColumn] = matchings [nextColumn];
                currentColumn = nextColumn;
            } while (width != currentColumn);
            
            display ();
        }
        printSeparator ();
        System .out .println ("Assignment cost: " + (-columnsPotential [width]));
    }
    
    private static void display () {
        int k, l;
        
        printSeparator ();
        System .out .println ("Iteration: " + iterationsCount);
        System .out .println ();
        
        for (k = 0; height > k; ++k) {
            if (rowIndex > k) {
                System .out .print ("v ");
            } else if (rowIndex == k) {
                System .out .print ("> ");
            } else {
                System .out .print ("  ");
            }
            for (l = 0; width > l; ++l) {
                printValue (weights [k] [l], k == matchings [l]);
            }
            System .out .print ("   ~ ");
            printValue (rowsPotential [k], k == matchingRow);
            System .out .println ();
        }
        System .out .print ("  ");
        for (l = 0; width > l; ++l) {
            System .out .print ("   | ");
        }
        System .out .print ("       Rows potential\n  ");
        for (l = 0; width > l; ++l) {
            printValue (auxMinima [l], false);
        }
        System .out .print ("       Auxiliary minima\n  ");
        for (l = 0; width > l; ++l) {
            printValue (wayBack [l], false);
        }
        System .out .print ("       Way back\n  ");
        for (l = 0; width >= l; ++l) {
            printValue (columnsPotential [l], l == nextColumn);
        }
        System .out .print ("  Columns potential\n  ");
        for (l = 0; width >= l; ++l) {
            if (usedColumns [l]) {
                System .out .print ("   + ");
            } else {
                System .out .print ("     ");
            }
        }
        System .out .print ("  Used columns\n  ");
        for (l = 0; width >= l; ++l) {
            printValue (matchings [l], false);
        }
        System .out .println ("  Column-row matching");
        System .out .println ();
    }
    
    private static void printValue (int value, boolean flag) {
        if (Integer .MAX_VALUE == value) {
            if (flag) {
                System .out .print ("[INF]");
            } else {
                System .out .print (" INF ");
            }
        } else {
            if (flag) {
                System .out .print (String .format ("%4s]", "[" + value));
            } else {
                System .out .print (String .format ("%4d ", value));
            }
        }
    }
    
    private static void printSeparator () {
        System .out .println ("========================================");
        System .out .println ();
    }
}
 

Программа выдаёт примерно такой листинг, по которому можно отслеживать этапы работы и принимаемые решения:

Используется синтаксис Text

========================================

Iteration: 1

>    3    7    3   13    9    ~   [0]
    19   13   19   12    7    ~    0 
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     3    7    3   13    9        Auxiliary minima
     5    5    5    5    5        Way back
    [0]   0    0    0    0    0   Columns potential
                              +   Used columns
    -1   -1   -1   -1   -1    0   Column-row matching

Delta: 3
========================================

Iteration: 1

>    3    7    3   13    9    ~   [3]
    19   13   19   12    7    ~    0 
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0    4    0   10    6        Auxiliary minima
     5    5    5    5    5        Way back
    [0]   0    0    0    0   -3   Columns potential
                              +   Used columns
    -1   -1   -1   -1   -1    0   Column-row matching

========================================

Iteration: 1

>   [3]   7    3   13    9    ~   [3]
    19   13   19   12    7    ~    0 
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0    4    0   10    6        Auxiliary minima
     5    5    5    5    5        Way back
     0    0    0    0    0  [-3]  Columns potential
                              +   Used columns
     0   -1   -1   -1   -1    0   Column-row matching

========================================

Iteration: 2

v   [3]   7    3   13    9    ~    3 
>   19   13   19   12    7    ~   [0]
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
    19   13   19   12    7        Auxiliary minima
     5    5    5    5    5        Way back
     0    0    0    0   [0]  -3   Columns potential
                              +   Used columns
     0   -1   -1   -1   -1    1   Column-row matching

Delta: 7
========================================

Iteration: 2

v   [3]   7    3   13    9    ~    3 
>   19   13   19   12    7    ~   [7]
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
    12    6   12    5    0        Auxiliary minima
     5    5    5    5    5        Way back
     0    0    0    0   [0] -10   Columns potential
                              +   Used columns
     0   -1   -1   -1   -1    1   Column-row matching

========================================

Iteration: 2

v   [3]   7    3   13    9    ~    3 
>   19   13   19   12   [7]   ~   [7]
     3   14    4   15    7    ~    0 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
    12    6   12    5    0        Auxiliary minima
     5    5    5    5    5        Way back
     0    0    0    0    0 [-10]  Columns potential
                              +   Used columns
     0   -1   -1   -1    1    1   Column-row matching

========================================

Iteration: 3

v   [3]   7    3   13    9    ~    3 
v   19   13   19   12   [7]   ~    7 
>    3   14    4   15    7    ~   [0]
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     3   14    4   15    7        Auxiliary minima
     5    5    5    5    5        Way back
    [0]   0    0    0    0  -10   Columns potential
                              +   Used columns
     0   -1   -1   -1    1    2   Column-row matching

Delta: 3
========================================

Iteration: 3

v   [3]   7    3   13    9    ~    3 
v   19   13   19   12   [7]   ~    7 
>    3   14    4   15    7    ~   [3]
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0   11    1   12    4        Auxiliary minima
     5    5    5    5    5        Way back
    [0]   0    0    0    0  -13   Columns potential
                              +   Used columns
     0   -1   -1   -1    1    2   Column-row matching

========================================

Iteration: 4

v   [3]   7    3   13    9    ~   [3]
v   19   13   19   12   [7]   ~    7 
>    3   14    4   15    7    ~    3 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0    4    0   10    4        Auxiliary minima
     5    0    0    0    5        Way back
     0    0   [0]   0    0  -13   Columns potential
     +                        +   Used columns
     0   -1   -1   -1    1    2   Column-row matching

Delta: 0
========================================

Iteration: 4

v   [3]   7    3   13    9    ~   [3]
v   19   13   19   12   [7]   ~    7 
>    3   14    4   15    7    ~    3 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0    4    0   10    4        Auxiliary minima
     5    0    0    0    5        Way back
     0    0   [0]   0    0  -13   Columns potential
     +                        +   Used columns
     0   -1   -1   -1    1    2   Column-row matching

========================================

Iteration: 4

v    3    7   [3]  13    9    ~   [3]
v   19   13   19   12   [7]   ~    7 
>   [3]  14    4   15    7    ~    3 
    17   13    4   17    6    ~    0 
     |    |    |    |    |        Rows potential
     0    4    0   10    4        Auxiliary minima
     5    0    0    0    5        Way back
     0    0    0    0    0 [-13]  Columns potential
     +                        +   Used columns
     2   -1    0   -1    1    2   Column-row matching

========================================

Iteration: 5

v    3    7   [3]  13    9    ~    3 
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~    3 
>   17   13    4   17    6    ~   [0]
     |    |    |    |    |        Rows potential
    17   13    4   17    6        Auxiliary minima
     5    5    5    5    5        Way back
     0    0   [0]   0    0  -13   Columns potential
                              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

Delta: 4
========================================

Iteration: 5

v    3    7   [3]  13    9    ~    3 
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~    3 
>   17   13    4   17    6    ~   [4]
     |    |    |    |    |        Rows potential
    13    9    0   13    2        Auxiliary minima
     5    5    5    5    5        Way back
     0    0   [0]   0    0  -17   Columns potential
                              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

========================================

Iteration: 6

v    3    7   [3]  13    9    ~   [3]
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~    3 
>   17   13    4   17    6    ~    4 
     |    |    |    |    |        Rows potential
     0    4    0   10    2        Auxiliary minima
     2    2    5    2    5        Way back
    [0]   0    0    0    0  -17   Columns potential
               +              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

Delta: 0
========================================

Iteration: 6

v    3    7   [3]  13    9    ~   [3]
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~    3 
>   17   13    4   17    6    ~    4 
     |    |    |    |    |        Rows potential
     0    4    0   10    2        Auxiliary minima
     2    2    5    2    5        Way back
    [0]   0    0    0    0  -17   Columns potential
               +              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

========================================

Iteration: 7

v    3    7   [3]  13    9    ~    3 
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~   [3]
>   17   13    4   17    6    ~    4 
     |    |    |    |    |        Rows potential
     0    4    0   10    2        Auxiliary minima
     2    2    5    2    5        Way back
     0    0    0    0   [0] -17   Columns potential
     +         +              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

Delta: 2
========================================

Iteration: 7

v    3    7   [3]  13    9    ~    5 
v   19   13   19   12   [7]   ~    7 
v   [3]  14    4   15    7    ~   [5]
>   17   13    4   17    6    ~    6 
     |    |    |    |    |        Rows potential
     0    2    0    8    0        Auxiliary minima
     2    2    5    2    5        Way back
    -2    0   -2    0   [0] -19   Columns potential
     +         +              +   Used columns
     2   -1    0   -1    1    3   Column-row matching

========================================

Iteration: 8

v    3    7   [3]  13    9    ~    5 
v   19   13   19   12   [7]   ~   [7]
v   [3]  14    4   15    7    ~    5 
>   17   13    4   17    6    ~    6 
     |    |    |    |    |        Rows potential
     0    2    0    5    0        Auxiliary minima
     2    2    5    4    5        Way back
    -2   [0]  -2    0    0  -19   Columns potential
     +         +         +    +   Used columns
     2   -1    0   -1    1    3   Column-row matching

Delta: 2
========================================

Iteration: 8

v    3    7   [3]  13    9    ~    7 
v   19   13   19   12   [7]   ~   [9]
v   [3]  14    4   15    7    ~    7 
>   17   13    4   17    6    ~    8 
     |    |    |    |    |        Rows potential
     0    0    0    3    0        Auxiliary minima
     2    2    5    4    5        Way back
    -4   [0]  -4    0   -2  -21   Columns potential
     +         +         +    +   Used columns
     2   -1    0   -1    1    3   Column-row matching

========================================

Iteration: 8

v    3   [7]   3   13    9    ~    7 
v   19   13   19   12   [7]   ~   [9]
v   [3]  14    4   15    7    ~    7 
>   17   13   [4]  17    6    ~    8 
     |    |    |    |    |        Rows potential
     0    0    0    3    0        Auxiliary minima
     2    2    5    4    5        Way back
    -4    0   -4    0   -2 [-21]  Columns potential
     +         +         +    +   Used columns
     2    0    3   -1    1    3   Column-row matching

========================================

Assignment cost: 21
 

К сожалению, я так и не въехал в алгоритм на столько, чтобы повторить его с нуля по памяти. Видать ещё нужно время и несколько заходов, чтобы его до конца раскурить.

Так же, пока для меня остаётся открытым вопрос, можно ли в матрице исходных данных использовать величину Integer .MAX_VALUE в качестве "бесконечного" веса-затычки для тех назначений работник-работа, которые по условию невозможны, либо же это приведёт к переполнению в вычислениях и ошибке/зависанию программы. По идее, пока в каждой строке и в каждом столбце есть по одному обычному числу, решение существует и должно находиться.

[ljgdasfhk]

Посмотрите на это :

Используется синтаксис C

/**
 * Метод Cost Scaling, переделанный.
 * страница 28-29 (Algorithm 6, 7 и 8)
 */

#include <windows.h>
#include <stdio.h>
#include <string.h>
#include <tchar.h>

typedef long long int64;

const int N = 2048;             // Максимальный размер матрицы плюс 1
const int64 oo = ( 1ll << 62 ); // Бесконечность

const int CONSTR_N = 2000;      // Ограничение задачи по n
const int CONSTR_CIJ = 1073741; // Ограничение задачи по |C_{ij}|

/* Буфер для файла ( с запасом ) */
/* Читать будем через отображение в память */
const int BUF_SIZE = 10 * CONSTR_N * CONSTR_N;

char * str;

int n,                // Порядок матрицы
    p [ N ];          // Назначение

int64 C [ N ] [ N ],  // Матрица
      pi [ N ];       // Потенциалы

int64 Eps;            // Масштаб

/**
 * Функции для получения числа из памяти
 */
inline int isDigit ( char c ) {
        return ( c >= '0' && c <= '9' );
}

inline int isNumber ( char c ) {
        return ( c == '-' || isDigit ( c ) );
}

inline int getInt ( char ** str ) {
        int res = 0, s = 1;
        while ( ! isNumber ( ** str ) )
                ( * str ) ++;
        if ( ** str == '-' ) {
                s = -1;
                ( * str ) ++;
        }
  while ( isDigit ( ** str ) ) {
        res *= 10;
        res += ( ** str ) - '0';
        ( * str ) ++;
  }
  return res * s;
}

/**
 * Ввод данных через отображения файла в память.
 */
int Read ( ) {
        HANDLE hFile, mFile;
        LPVOID pBuf;

        hFile = CreateFile ( _T ( "input.txt" ), GENERIC_READ, FILE_SHARE_READ, NULL, OPEN_EXISTING, FILE_ATTRIBUTE_NORMAL, 0 );
        if ( hFile == INVALID_HANDLE_VALUE ) {
                fprintf ( stderr, "Problems with opening file\n" );
                return 0;
        }
        mFile = CreateFileMapping ( hFile, NULL, PAGE_READONLY, 0, 0, 0 );
        if ( mFile == NULL ) {
                CloseHandle ( hFile );
                fprintf ( stderr, "Problems with mapping file\n" );
                return 0;
        }
        pBuf = MapViewOfFile ( mFile, FILE_MAP_READ, 0, 0, 0);
        if ( pBuf == NULL ) {
                fprintf ( stderr, "Problems with viewing file\n" );
                CloseHandle ( hFile );
                CloseHandle ( mFile );
                return 0;
        }

        str = ( char * ) pBuf;

        n = getInt ( & str );

  /* Читаем транспонированную матрицу */
  for ( int i = 1; i <= n; i ++ )
        for ( int j = 1; j <= n; j ++ )
        C [ j ] [ i ] = getInt ( & str );

        CloseHandle ( hFile );
        CloseHandle ( mFile );

        return 1;
}

/**
 * Поиск в строке s остаточной матрицы
 * первого и второго минимумов.
 * Возвращяет позицию первого минимума.
 * Через ссылки возвращяет сами значения min1 и min2
 * Работает только когда n > 1
 */
int getTwoMins ( int s, int64 & min1, int64 & min2 ) {
        int t, j;
        int64 C_pi;
        min1 = oo, min2 = oo;
        for ( t = 1; t <= n; t ++ ) {
                C_pi = C [ s ] [ t ] + pi [ t ]; // Остаточная цена (residual cost)
                if ( C_pi < min1 ) {
                        min2 = min1;
                        min1 = C_pi;
                        j = t;
                }
                else if ( C_pi < min2 ) {
                        min2 = C_pi;
                }
        }
        return j;
}

/**
 * Эта функция отличается от приведённой в источнике
 * Вместо того, чтобы проталкивать из каждой активной вершины
 * в произвольном порядке,
 * сразу проталкиваем поток из всех верших,
 * с которыми произошла коллизия в процессе текущего назначения
 */
void DoublePush ( int s ) {
        int j, tmp;
        int64 min1, min2;

        // Идём по дереву коллизий
        while ( s ) {

                j = getTwoMins ( s, min1, min2 );

                // Пересчёт потенциалов. Здесь было так
                // pi [ j ] = pi [ k ] + C [ s ] [ k ] - C [ s ] [ j ] + Eps;
    // где j и k - номера первого и второго минимумов
    // Но после упрощения
    // стало так:
    pi [ j ] += min2 - min1 + Eps;

    /* Поменять местами s и pi [ j ] */
                tmp = s;        // Старое s сохраним на время куда-нибудь
                s = p [ j ];    // Если есть коллизия, то s будет больше 0
                p [ j ] = tmp;  // В любом случае присваеваем новое назначение столбцу j
        }
}

/**
 * Исправить 2*Eps-оптимальный поток --- сделать его Eps-оптимальным
 */
void ImproveApproximation ( ) {
        int i, j;

  /* Сначала назначений нет */
        memset ( p + 1, 0, sizeof ( p [ 0 ] ) * n );

  /* Найти назначение для каждого элемента */
  for ( i = 1; i <= n; i ++ )
                DoublePush ( i );
}

/**
 * Этого чуда почему-то не нашёл
 */
int64 abs64 ( int64 a ) {
        if ( a < 0 )
                return -a;
        return a;
}

int main()  {

        int i, j;

        if ( ! Read ( ) ) {
                fprintf ( stderr, "Problems with reading from file\n" );
                return 0;
        }

        /**
         * Теоретически поиск двух минимумов не работает,
   * когда один элемент. Поэтому от греха подальше
   * рассмотрим данный случай отдельно
         */
        if ( n == 1 ) {
                p [ 1 ] = 1;
                goto output;  // Что?.. Так нельзя? Не, не знал об этом...
        }

  /**
   * Умножить все элементы на n и заодно
   * отыскать ближайшую степень двойки
   */
        Eps = 1;
        for ( i = 1; i <= n; i ++ )
                for ( j = 1; j <= n; j ++ ) {
                        C [ i ] [ j ] *= n;
                        while ( Eps < abs64 ( C [ i ] [ j ] ) )
                                Eps *= 2;
                }

        /**
         * Алгорим Cost Scaling
         */
        Eps *= 2;
        while ( Eps /= 2 )
                ImproveApproximation ( );
  /* Конец алгоритма Cost Scaling */

  /**
   * Вывод ответа
   */
output:

  /* Посчитать ответ */
        int64 ans = 0;
        for ( i = 1; i <= n; i ++ )
                ans += C [ p [ i ] ] [ i ] / n;

        /* Вывести ответ */
        /* !!! Поменять `%I64d' на `%lld', если вы в Linux'e */
        freopen ( "output.txt", "w", stdout );
        printf ( "%I64d\n", ans );
        for ( i = 1; i <= n; i ++ )
                printf ( "%d ", p [ i ] );
        putchar ( '\n' );

        return 0;
}
 

Статья

[B@R5uk]

Цитата:

It is worth noting, however, that shortest augmenting path algorithms tackle certain configurations more efficiently than push/relabel or auction algorithms. Therefore, Ahuja and Orlin [OA92] propose a hybrid algorithm, which in each scaling iteration first starts with an auction and then, if no complete assignment has been found after a certain amount of bidding steps, switches to a shortest augmenting path method. This hybrid algorithm matches the best known running time bound of $O(\sqrt{n}m\log(nC))$.

One of the oldest algorithms for the assignment problem, the Hungarian method [Kuh55], works with shortest augmenting paths as well. In its original version, it was proposed for a complete bipartite graph, but it can also be applied to sparse graphs efficiently (see [AMO93]). It still has the best strongly polynomial time bound for the assignment problem ($O(nm + n^2\log n)$) if using Dijkstra’s algorithm with Fibonacci heaps for finding shortest paths). In practical usage, however, it is not competitive compared to recent algorithms.

Ха!

ljgdasfhk, как работает алгоритм и почему, мне, конечно, ещё вникать и вникать, но за статью большое СПАСИБО! Прямо таки расширился горизонт познания, появились новые направления, в которые копать. Это касается и существующих разновидностях задачи о назначениях, и подлежащей теории линейного программирования с дуальной задачей, и самого факта существования более быстродействующих алгоритмов, чем венгерский.

Остаётся, правда, ещё открытым вопрос, на счёт скрытой константы в их временных сложностях. Другими словами, с каких величин n и m начинается практический выигрыш во времени по сравнению с простым венгерским алгоритмом?

[ljgdasfhk]

К двудольному графу с единичными пропускными способностями рёбер применяется алгоритм поиска потока минимальной стоимости. Вместо проталкивания предпотока из активных вершин в произвольном порядке, здесь выполняется проталкивание по очереди из всех вершин, которые начинают образовывать коллизи после проталкивания. Основная часть программы получается значительно короче венгерского метода. Узким местом здесь является поиск первого и второго минимумов. Чтобы его ускорить можно попробовать придумать какую-нибудь хитрую структуру данных.

[B@R5uk]

Читаю Rainer Burkard, Mauro Dell'Amico, Silvano Martello - Assignment problems. Две основных цели чтения — это понять, что вообще в этой области придумано, и найти вариант Венгерского алгоритма, который специально заточен под сильно разреженную матрицу стоимостей назначений. То есть, если $N$ — это число работ (строк в матрице или левых вершин в двудольном графе), а $N'>N$ — число доступных работников (столбцов или правых вершин в двудольном графе), из которых требуется подобрать оптимальное по стоимости назначение, то суммарное число всех доступных назначений $M$ (конечных стоимостей в матрице или рёбер в двудольном графе) удовлетворяет условию $M\ll N\times N'$.

Пока только нашёл (и чутка вник) интересные алгоритмы построения максимального паросочетания в двудольном графе. И их числе алгоритм Хопкрофта—Карпа, работающий за время $O\left(\sqrt{n}m\right)$, где n — число вершин в графе (всех: и левых, и правых), а m — число рёбер; а так же алгоритм Альта, Блюма, Мелхорна и Паула, который работает за время $O\left(n\sqrt{nm/\log n}\right)$. На И-максе аналогичный алгоритм Куна (самый простой из всех, правда) работает за время $O\left(nm\right)$. Алгоритмы поиска максимальных паросочетаний для меня пока представляют чисто познавательный интерес. Не представляю, куда их можно применить.

Так же прочитал и осознал, что предложенный выше пользователем ljgdasfhk алгоритм, использующий специальный приём, называемый "масштабирование стоимости" (cost scaling technique), и работающий за время $O(\sqrt{n}m\log(nC))$, можно применять не ко всем задачам, а только к тем, в которых веса рёбер (или элементы весовой матрицы) являются целыми числами. Здесь константа $C$ — это как раз максимальный разрешённый целочисленный вес ребра (или коэффициент в матрице).

[B@R5uk]

Что-то в книжке вообще нет варианта алгоритма, который по одной строчке обновляет решение, как это сделано в алгоритме Лопатина. Подправил его алгоритм, чтобы он работал с разреженной матрицей весов. Вернее, правильней будет сказать, навставлял в алгоритм костылей:

Используется синтаксис Java

import java.util.*;

public class Study_Hungarian_3 {
    
    private static final Random rng = new Random ();
    
    private static int width, height;
    private static int [] [] weights;
    private static int [] countByColumn;
    
    private static int rowIndex, columnIndex;
    private static int currentColumn, matchingRow, nextColumn;
    private static int value, delta, iterationsCount;
    
    private static int [] matchings, auxMinima, wayBack;
    private static int [] rowsPotential, columnsPotential;
    private static boolean [] usedColumns;
    
    public static void main(String[] args) {
        
        makeRandomTest (12, 8, 50, 2, 2);
        diplayWeights ();
        findAssignment ();
    }
    
    private static void makeRandomTest (int aWidth, int aHeight,
                                    int aMaxValue, int aMinCount, int aRandomCount) {
        int k, l, index;
        
        width   = aWidth;
        height  = aHeight;
        weights = new int [height] [width];
        
        for (k = 0; height > k; ++k) {
            Arrays .fill (weights [k], Integer .MAX_VALUE);
        }
        
        countByColumn = new int [width];
        
        for (k = 0; height > k; ++k) {
            for (l = 0; aMinCount > l; ++l) {
                index = findMinCountIndex ();
                weights [k] [index] = rng .nextInt (aMaxValue);
                ++countByColumn [index];
            }
            for (l = 0; aRandomCount > l; ) {
                index = rng .nextInt (width);
                if (Integer .MAX_VALUE != weights [k] [index]) {
                    continue;
                }
                weights [k] [index] = rng .nextInt (aMaxValue);
                ++countByColumn [index];
                ++l;
            }
        }
    }
    
    private static int findMinCountIndex () {
        int k, count, bestCount, bestIndex;
        
        bestCount = Integer .MAX_VALUE;
        bestIndex = -1;
        
        for (k = 0; width > k; ++k) {
            count = countByColumn [k];
            if (bestCount > count) {
                bestCount = count;
                bestIndex = k;
            }
        }
        
        return bestIndex;
    }
    
    private static void diplayWeights () {
        int k, l, value;
        
        System .out .println ();
        for (k = 0; height > k; ++k) {
            for (l = 0; width > l; ++l) {
                value = weights [k] [l];
                if (Integer .MAX_VALUE == value) {
                    System .out .print ("   -");
                } else {
                    System .out .print (String .format ("%4d", value));
                }
            }
            System .out .println ();
        }
        System .out .println ();
    }
    
    private static void findAssignment () {
        
        if (height > width) {
            throw new IllegalArgumentException ("Data height must be less than or equal data width.");
        }
        rowIndex         = -1;
        columnIndex      = -1;
        currentColumn    = -1;
        matchingRow      = -1;
        nextColumn       = -1;
        rowsPotential    = new int     [height];
        columnsPotential = new int     [width + 1];
        usedColumns      = new boolean [width + 1];
        matchings        = new int     [width + 1];
        auxMinima        = new int     [width];
        wayBack          = new int     [width];
        Arrays .fill (matchings, Integer .MAX_VALUE);
        
        iterationsCount = 0;
        for (rowIndex = 0; height > rowIndex; ++rowIndex) {
            //      Column with index {width} is fictitious
            matchings [width] = rowIndex;
            currentColumn = width;
            
            Arrays .fill (usedColumns, false);
            Arrays .fill (auxMinima, Integer .MAX_VALUE);
            Arrays .fill (wayBack,   Integer .MAX_VALUE);
            
            //      Looking for free column
            do {
                ++iterationsCount;
                
                usedColumns             [currentColumn] = true;
                matchingRow = matchings [currentColumn];
                delta = Integer .MAX_VALUE;
                
                //      Searching current matching row for the best next column
                
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = weights        [matchingRow] [columnIndex];
                    if (Integer .MAX_VALUE == value) {
                        continue;
                    }
                    value -= rowsPotential [matchingRow] +
                             columnsPotential            [columnIndex];
                    if (auxMinima [columnIndex] > value) {
                        auxMinima [columnIndex] = value;
                        wayBack   [columnIndex] = currentColumn;
                    }
                    if (delta > auxMinima [columnIndex]) {
                        delta = auxMinima [columnIndex];
                        nextColumn =       columnIndex;
                    }
                }
                
                display ("New Delta is found: " + delta);
                
                if (Integer .MAX_VALUE == delta) {
                    throw new IllegalArgumentException ("No assignment is possible.");
                }
                
                //      Recalculating potentials and auxiliary minima
                
                for (columnIndex = 0; width >= columnIndex; ++columnIndex) {
                    if (usedColumns              [columnIndex]) {
                        rowsPotential [matchings [columnIndex]] += delta;
                        columnsPotential         [columnIndex]  -= delta;
                    } else {
                        if (Integer .MAX_VALUE != auxMinima [columnIndex]) {
                            auxMinima            [columnIndex]  -= delta;
                        }
                    }
                }
                currentColumn = nextColumn;
                
                display ("Potentials and aux minima are recalculated");
                
            } while (Integer .MAX_VALUE != matchings [currentColumn]);
            
            //      Free column has been found, restoring new assignment using wayBack
            
            do {
                nextColumn = wayBack [currentColumn];
                matchings [currentColumn] = matchings [nextColumn];
                currentColumn = nextColumn;
            } while (width != currentColumn);
            
            display ("New assignment is formed");
        }
        printSeparator ();
        System .out .println ("Assignment cost: " + (-columnsPotential [width]));
    }
    
    private static void display (String arg) {
        int k, l;
        
        printSeparator ();
        System .out .println ("Iteration: " + iterationsCount + ". " + arg);
        System .out .println ();
        
        for (k = 0; height > k; ++k) {
            if (rowIndex > k) {
                System .out .print ("v ");
            } else if (rowIndex == k) {
                System .out .print ("> ");
            } else {
                System .out .print ("  ");
            }
            for (l = 0; width > l; ++l) {
                printValue (weights [k] [l], k == matchings [l]);
            }
            System .out .print ("   ~ ");
            printValue (rowsPotential [k], k == matchingRow);
            System .out .println ();
        }
        System .out .print ("  ");
        for (l = 0; width > l; ++l) {
            System .out .print ("   | ");
        }
        System .out .print ("       Rows potential\n  ");
        for (l = 0; width > l; ++l) {
            printValue (auxMinima [l], false);
        }
        System .out .print ("       Auxiliary minima\n  ");
        for (l = 0; width > l; ++l) {
            printValue (wayBack [l], false);
        }
        System .out .print ("       Way back\n  ");
        for (l = 0; width >= l; ++l) {
            printValue (columnsPotential [l], l == nextColumn);
        }
        System .out .print ("  Columns potential\n  ");
        for (l = 0; width >= l; ++l) {
            if (usedColumns [l]) {
                System .out .print ("   + ");
            } else {
                System .out .print ("     ");
            }
        }
        System .out .print ("  Used columns\n  ");
        for (l = 0; width >= l; ++l) {
            printValue (matchings [l], false);
        }
        System .out .println ("  Column-row matching");
        System .out .println ();
    }
    
    private static void printValue (int value, boolean flag) {
        if (Integer .MAX_VALUE == value) {
            if (flag) {
                System .out .print (" ### ");
            } else {
                System .out .print ("   - ");
            }
        } else {
            if (flag) {
                System .out .print (String .format ("%4s]", "[" + value));
            } else {
                System .out .print (String .format ("%4d ", value));
            }
        }
    }
    
    private static void printSeparator () {
        System .out .println ("================================================================================");
        System .out .println ();
    }
}
 

Вроде всё работает. Однако, у меня есть подозрение, что это жутко неоптимально не смотря на всего лишь кубическую сложность.

[B@R5uk]

Во всех разновидностях Венгерского алгоритма имеется два ключевых момента. Первый момент — это наличие неких величин, ассоциированных со столбцами и строками весовой матрицы и связанных с её значениями. На И-Максе и в вики они называются потенциалами, в англоязычной литературе их обзывают двойственными переменными (dual variables $u_i$ и $v_j$). Английское название имеет корни в теории линейного программирования (двойственная задача), сильно специализированным случаем которого является задача о назначениях. Второй момент — это наличие понятий теории двудольных графов, в частности паросочетаний и увеличивающих путей.

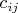В теории доказывается, что если потенциалы (или двойственные переменные) $u_i$ и $v_j$ такие, что редуцированные веса рёбер $\overline{c_{ij}}$, рассчитываемые на основе исходных весов $c_{ij}$ по формуле

$$\overline{c_{ij}}=c_{ij}-u_i-v_j$$

все неотрицательны, то паросочетание, проходящее по рёбрам с нулевым редуцированным весом, является оптимальным и доставляет решение задачи о назначениях. Рёбра с нулевым редуцированным весом у нас называются жёсткими, а в англоязычной литературе — удовлетворяющими "complementary slackness conditions".

Задача Венгерского алгоритма, таким образом, заключается в том, чтобы строить всё большее и большее паросочетание из жёстких рёбер, используя для этого метод увеличивающего пути и, возможно, попутно корректно пересчитывая потенциалы (двойственные переменные), чтобы, при необходимости, выявлять новые жёсткие рёбра для построения паросочетаний; до тех пор, пока, наконец, не будет найдено решение (в каждой строчке выбрана допустимая ячейка), или не выяснится, что таковых не существует (в случае сильно разреженной матрицы весов).

Трудоёмкость алгоритма накапливается в двух местах: поиск увеличивающего пути и перерасчёт потенциалов. Часто так бывает, что при назначении решения в очередной строчке увеличивающий путь содержит всего лишь одно ребро (соответствующее одной добавляемой в решение ячейке этой строчки), но чтобы установить этот факт приходится пройтись по всем другим ранее обработанным строчкам.

Алгоритм с И-Макса, который я на все лады переиначивал в этой теме, производит перерасчёт потенциалов после каждого обращения к новой строчке матрицы, в том числе в процессе поиска увеличивающего пути (цикл после комментария Recalculating potentials and auxiliary minima). То есть, проходя по ранее обработанным строчкам в довесок для каждого прохода он пересчитывает потенциалы, что является ещё одним проходом по всей ширине строчки. И это очень нерационально. Более того, это не позволяет воспользоваться тем, что матрица весов может быть сильно разреженной, что, по идее, должно было бы сильно снизить трудоёмкость алгоритма.

Вот практический пример такого случая (при добавлении в решение 8-й строчки алгоритм просматривает ещё 4 строчки из 7 предыдущих, попутно пересчитывая потенциалы):

Используется синтаксис Text

================================================================================

Iteration: 18. New assignment is formed

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~  [33]
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
>    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
    41    -    -    -    -    -   28    -   20    -    -   37    ~    0 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
     4    0   15    0    0   17   18   29    0    0    0   10        Auxiliary minima
     9    4    3   12    3    4    3   12    1    8    9    1        Way back
     0    1    0   -1    8    0    0    0   -7  -13    0    0 [-94]  Columns potential
          +         +    +                   +    +              +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    6   Column-row matching

================================================================================

Iteration: 19. New Delta is found: 27

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   [0]
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    41    -    -    -    -    -   28    -   27    -    -   37        Auxiliary minima
    12    -    -    -    -    -   12    -   12    -    -   12        Way back
     0    1    0   -1    8    0    0    0  [-7] -13    0    0  -94   Columns potential
                                                                 +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 19. Potentials and aux minima are recalculated

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~  [27]
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    14    -    -    -    -    -    1    -    0    -    -   10        Auxiliary minima
    12    -    -    -    -    -   12    -   12    -    -   12        Way back
     0    1    0   -1    8    0    0    0  [-7] -13    0    0 -121   Columns potential
                                                                 +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 20. New Delta is found: 0

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~  [20]
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0    -    -    -    -    1    -    0    -    -   10        Auxiliary minima
     8    8    -    -    -    -   12    -   12    -    -   12        Way back
     0   [1]   0   -1    8    0    0    0   -7  -13    0    0 -121   Columns potential
                                             +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 20. Potentials and aux minima are recalculated

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~  [20]
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0    -    -    -    -    1    -    0    -    -   10        Auxiliary minima
     8    8    -    -    -    -   12    -   12    -    -   12        Way back
     0   [1]   0   -1    8    0    0    0   -7  -13    0    0 -121   Columns potential
                                             +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 21. New Delta is found: 0

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~  [14]
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0    -    -    0   17    1    -    0   28    -   10        Auxiliary minima
     8    8    -    -    1    1   12    -   12    1    -   12        Way back
     0    1    0   -1   [8]   0    0    0   -7  -13    0    0 -121   Columns potential
          +                                  +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 21. Potentials and aux minima are recalculated

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~  [14]
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0    -    -    0   17    1    -    0   28    -   10        Auxiliary minima
     8    8    -    -    1    1   12    -   12    1    -   12        Way back
     0    1    0   -1   [8]   0    0    0   -7  -13    0    0 -121   Columns potential
          +                                  +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 22. New Delta is found: 0

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~  [14]
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0   15    0    0   17    1    -    0   28    -   10        Auxiliary minima
     8    8    4    4    1    1   12    -   12    1    -   12        Way back
     0    1    0  [-1]   8    0    0    0   -7  -13    0    0 -121   Columns potential
          +              +                   +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 22. Potentials and aux minima are recalculated

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~  [14]
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~    4 
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0   15    0    0   17    1    -    0   28    -   10        Auxiliary minima
     8    8    4    4    1    1   12    -   12    1    -   12        Way back
     0    1    0  [-1]   8    0    0    0   -7  -13    0    0 -121   Columns potential
          +              +                   +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 23. New Delta is found: 1

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   20 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   14 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   14 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~   [4]
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   27 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    13    0   15    0    0   17    1   29    0   28    -   10        Auxiliary minima
     8    8    4    4    1    1   12    3   12    1    -   12        Way back
     0    1    0   -1    8    0   [0]   0   -7  -13    0    0 -121   Columns potential
          +         +    +                   +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 23. Potentials and aux minima are recalculated

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   21 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   15 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   15 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~   [5]
>   41    -    -    -    -    -   28    -   20    -    -   37    ~   28 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    12    0   14    0    0   16    0   28    0   27    -    9        Auxiliary minima
     8    8    4    4    1    1   12    3   12    1    -   12        Way back
     0    0    0   -2    7    0   [0]   0   -8  -13    0    0 -122   Columns potential
          +         +    +                   +                   +   Used columns
     -    5    -    6    1    2    -    -    0    3    4    -    7   Column-row matching

================================================================================

Iteration: 23. New assignment is formed

v   33   21    -    -    -    -    -    -  [13]   -    -   30    ~   21 
v    -    -   29   13  [22]   -   32    -    -    -    -    -    ~   15 
v    -    -   40    -    -   [7]   -   29   49    -    -    -    ~    7 
v    -   28    -    -    -    -    -    -    7   [1]  22    -    ~   14 
v   37    -    -   32    -    -    -    -    -   20  [33]   -    ~   33 
v    -  [15]   -    -   22   31    -    -    -   29    -    -    ~   15 
v    -    -    -   [3]  41    -   33   33    -    -    -    -    ~   [5]
>   41    -    -    -    -    -  [28]   -   20    -    -   37    ~   28 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
    12    0   14    0    0   16    0   28    0   27    -    9        Auxiliary minima
     8    8    4    4    1    1   12    3   12    1    -   12        Way back
     0    0    0   -2    7    0    0    0   -8  -13    0    0 [-122]  Columns potential
          +         +    +                   +                   +   Used columns
     -    5    -    6    1    2    7    -    0    3    4    -    7   Column-row matching

================================================================================

Assignment cost: 122
 

[B@R5uk]

B@R5uk в сообщении #1498537 писал(а):

Вроде всё работает.

Нет, не работает. Где-то я в процессе модификации допустил логическую ошибку. Алгоритм находит решение, но оно не всегда является оптимальным, хотя и близко к нему.

Я внёс для удобства повторения случайных результатов такую вот модификацию в код:

Используется синтаксис Java

public class Study_Hungarian_3 {
    
    private static final Random rng = new Random (4);
    
    //    ............
    
    public static void main (String [] args) {
        
        makeRandomTest (12, 9, 50, 3, 1);
        diplayWeights ();
        findAssignment ();
    }
    
    private static void makeRandomTest (int aWidth, int aHeight,
                                    int aMaxValue, int aRandomCount, int aMinCount) {
        int k, l, index;
        
        width   = aWidth;
        height  = aHeight;
        weights = new int [height] [width];
        
        for (k = 0; height > k; ++k) {
            Arrays .fill (weights [k], Integer .MAX_VALUE);
        }
        
        countByColumn = new int [width];
        
        for (k = 0; height > k; ++k) {
            for (l = 0; aRandomCount > l; ) {
                index = rng .nextInt (width);
                if (Integer .MAX_VALUE != weights [k] [index]) {
                    continue;
                }
                weights [k] [index] = rng .nextInt (aMaxValue);
                ++countByColumn [index];
                ++l;
            }
            for (l = 0; aMinCount > l; ++l) {
                index = findMinCountIndex ();
                weights [k] [index] = rng .nextInt (aMaxValue);
                ++countByColumn [index];
            }
        }
    }
    
    //    ............
}
 

Алгоритм выдаёт в качестве решения:

Используется синтаксис Text

================================================================================

Iteration: 16. New assignment is formed

v   46    -    2   [8]   -    -    -    -    -   11    -    -    ~   17 
v    -   19   [2]   -    -    -   27    -    8    -    -    -    ~   17 
v  [12]   -    -    -   39    -    -    -    -    -    3   19    ~   12 
v    -    -    -   33    -   41    -   44    -    -  [33]   -    ~   42 
v    -  [32]  45    -   33   34    -    -    -    -    -    -    ~   32 
v   16    -    -    -    -    -    6    -    -   46    -   [2]   ~    2 
v   44   32    -    -    -   14    -   [8]   -    -    -    -    ~    8 
v   26    -    -    -    -    -    -    -   [2]  36   36    -    ~   11 
>    9   35    -   27    -    -    -    -    -   [1]   -    -    ~   [1]
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
     8   34    -   35    -    -    -    -    -    0    -    -        Auxiliary minima
    12   12    -   12    -    -    -    -    -   12    -    -        Way back
     0    0  -15   -9    0    0    0    0   -9    0   -9    0 [-100]  Columns potential
                                                                 +   Used columns
     2    4    1    0    -    -    -    6    7    8    3    5    8   Column-row matching

================================================================================

Assignment cost: 100
 

Хотя оптимальным является такое назначение (вроде бы, во всяком случае оно лучше):

Используется синтаксис Text

  46    -    2   [8]   -    -    -    -    -   11    -    - 
   -   19   [2]   -    -    -   27    -    8    -    -    - 
  12    -    -    -   39    -    -    -    -    -   [3]  19 
   -    -    -   33    -  [41]   -   44    -    -   33    - 
   -  [32]  45    -   33   34    -    -    -    -    -    - 
  16    -    -    -    -    -    6    -    -   46    -   [2]
  44   32    -    -    -   14    -   [8]   -    -    -    - 
  26    -    -    -    -    -    -    -   [2]  36   36    - 
   9   35    -   27    -    -    -    -    -   [1]   -    - 
 

И где, спрашивается, теперь мне искать ошибку?

[B@R5uk]

B@R5uk в сообщении #1498921 писал(а):

И где, спрашивается, теперь мне искать ошибку?

Оказывается, дело в том что я, добавив запрещённые назначения, не совсем корректно модернизировал поиск оптимального столбца. В цикле, который идёт после комментария Searching current matching row for the best next column, на самом деле делается немного не то, что написано в этом комментарии. А именно, там производится две вещи: 1) обновление вспомогательных минимумов, указывающих, в каком направлении искать оптимальный свободный столбец и 2) собственно поиск этого столбца. Первая операция производится по разрешённым назначениям текущей строчки, а вторая — по всем ещё не задействованным элементам массива вспомогательных минимумов. Вставив отсев запрещённых назначений перед поиском оптимального столбца, я нечаянно отсеял некоторые оптимальные решения.

Правильно будет вместо кода такого:

Используется синтаксис Java

               
                //      Searching current matching row for the best next column
               
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = weights        [matchingRow] [columnIndex];
                    if (Integer .MAX_VALUE == value) {
                        continue;
                    }
                    value -= rowsPotential [matchingRow] +
                             columnsPotential            [columnIndex];
                    if (auxMinima [columnIndex] > value) {
                        auxMinima [columnIndex] = value;
                        wayBack   [columnIndex] = currentColumn;
                    }
                    if (delta > auxMinima [columnIndex]) {
                        delta = auxMinima [columnIndex];
                        nextColumn =       columnIndex;
                    }
                }
               
 

использовать код такой:

Используется синтаксис Java

                
                //      Updating aux minima with current row and searching for the next best column
                
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = weights            [matchingRow] [columnIndex];
                    if (Integer .MAX_VALUE != value) {
                        value -= rowsPotential [matchingRow] +
                                columnsPotential            [columnIndex];
                        if (auxMinima [columnIndex] > value) {
                            auxMinima [columnIndex] = value;
                            wayBack   [columnIndex] = currentColumn;
                        }
                    }
                    if (delta > auxMinima [columnIndex]) {
                        delta = auxMinima [columnIndex];
                        nextColumn =       columnIndex;
                    }
                }
                
 

Тогда и результат получается правильным:

Используется синтаксис Text

================================================================================

Iteration: 21. New assignment is formed

v   46    -    2   [8]   -    -    -    -    -   11    -    -    ~   16 
v    -   19   [2]   -    -    -   27    -    8    -    -    -    ~   16 
v   12    -    -    -   39    -    -    -    -    -   [3]  19    ~  [11]
v    -    -    -   33    -  [41]   -   44    -    -   33    -    ~   41 
v    -  [32]  45    -   33   34    -    -    -    -    -    -    ~   32 
v   16    -    -    -    -    -    6    -    -   46    -   [2]   ~    2 
v   44   32    -    -    -   14    -   [8]   -    -    -    -    ~    8 
v   26    -    -    -    -    -    -    -   [2]  36   36    -    ~   10 
>    9   35    -   27    -    -    -    -    -   [1]   -    -    ~    6 
     |    |    |    |    |    |    |    |    |    |    |    |        Rows potential
     1    3    0    0   28    0   11    3    0    0    0    8        Auxiliary minima
    10    2    9    9   10    3    2    3    2   12    3   10        Way back
     0    0  -14   -8    0    0    0    0   -8   -5   -8    0 [-99]  Columns potential
               +    +                        +    +    +         +   Used columns
     -    4    1    0    -    3    -    6    7    8    2    5    8   Column-row matching

================================================================================

Assignment cost: 99
 

Хотя этот поиск оптимального столбца по всей ширине матрицы вставляет ещё одну палку в колесо велосипеда оптимальности: ну совсем никак не получается воспользоваться разреженностью матрицы весов.

[B@R5uk]

В книге Burkard, Dell'Amico, Martello - Assignment problems нашёл таки интересный алгоритм в разделе 4.4. Это тоже вариант Венгерского алгоритма, использующий метод кратчайшего пути. В книге предлагается такой псевдокод:

\begin{tabular}{l} $\textbf{Algorithm 4.9. Procedure Shortest\_path}\;\left(k\right).\\ $\text{Find a shortest path in the incremental graph.}\\ $\\ $\textbf{for each}\;j\in V\;\textbf{do}\;\pi_j:=+\infty;\\ $SU:=SV:=\emptyset;\\ $sink:=0,\;\delta:=0,\;i:=k;\\ $\textbf{while}\;sink=0\;\textbf{do}\\ $\qquad SU:=SU\cup\left\{i\right\}; \\ $\qquad\textbf{for each}\;j\in V\;\verb|\|\;SV:\;\pi_j>\delta+c_{ij}-u_i-v_j\;\textbf{do}\\ $\qquad\qquad pred\left(j\right):=i,\;\pi_j:=\delta+c_{ij}-u_i-v_j\\ $\qquad\textbf{endfor};\\ $\qquad j:=\arg\min\left\{\pi_h:h\in V\;\verb|\|\;SV\right\};\\ $\qquad SV:=SV\cup\left\{j\right\},\;\delta:=\pi_j;\\ $\qquad\textbf{if}\;row\left(j\right)=0\;\textbf{then}\;sink:=j\\ $\qquad\textbf{else}\;i:=row\left(j\right)\\ $\textbf{endwhile};\\ $\textbf{comment:}\;\text{dual update};\\ $u_k:=u_k+\delta;\\ $\textbf{for each}\;i\in SU\;\verb|\|\;\left\{k\right\}\;\textbf{do}\;u_i:=u_i+\delta-\pi_{\varphi\left(i\right)};\\ $\textbf{for each}\;j\in SV\;\textbf{do}\;v_j:=v_j-\delta+\pi_j\\ $\textbf{return}\;sink\\ \end{tabular}


\begin{tabular}{l} $\textbf{Algorithm 4.10. Hungarian\_SP.}\\ $\text{Shortest path implementation of the Hungarian algorithm.}\\ $\\ $\text{initialize}\;u,\;v,\;row,\;\varphi\;\text{and}\;\overline{U};\\ $\textbf{while}\;\left|\overline{U}\right|<n\;\textbf{do}\\ $\qquad\text{let}\;k\;\text{be any vertex in}\;U\;\verb|\|\;\overline{U};\\ $\qquad sink:=\text{Shortest\_path}\;\left(k\right);\\ $\qquad U:=U\cup\left\{k\right\},\;j:=sink;\\ $\qquad\textbf{repeat}\\ $\qquad\qquad i:=pred\left(j\right),\;row\left(j\right):=i,\;h:=\varphi\left(i\right),\;\varphi\left(i\right):=j,\;j:=h\\ $\qquad\textbf{until}\;i=k\\ $\textbf{endwhile};\\ \end{tabular}

Алгоритм хорош уже хотя бы тем, что обновление потенциалов делает после нахождения кратчайшего удлиняющего пути. Надо заметить, что здесь есть некоторая двухсмысленность: слово кратчайший подразумевает суммарный вес пути, а удлиняющий — суммарное число рёбер в пути. Первая величина должна быть наименьшей из возможных, а вторая — нечётной: число нечётных свободных рёбер должно быть на единицу больше числа четных рёбер, принадлежащих паросочетанию. Тогда можно сделать замену одних на другие, и мощность паросочетания возрастёт на единицу, а соответствующее частичное решение будет оптимальным.

В целом, если вложить первую процедуру во вторую, алгоритм весьма похож на алгоритм с И-Макса. Даже внешний цикл можно сделать таким, чтобы он по очереди добавлял строки матрицы в решение одну за другой в порядке нумерации. Тут, правда, есть одна тонкость: если исходные веса матрицы гарантированно неотрицательные, то потенциалы можно просто инициализировать нулями. Эти значения будут корректными, а по мере работы алгоритм сам обновит значения до нужных, чтобы получить жёсткие рёбра. Если же в матрице имеются отрицательные веса, то необходимо сделать инициализацию потенциалов: пройтись по строкам или столбцам матрицы (или по тем и по другим), найти минимумы и инициализировать ими соответствующие потенциалы. Тогда на момент начала работы алгоритма они будут корректными. Книга ещё рекомендует сделать каким-нибудь жадным алгоритмом предварительные назначения.

Алгоритм Лопатина же всё делает сразу: потенциалы обновляются в процессе поиска пути. В этом плане там вообще творится какая-то уличная магия. Может случиться так, что после очередного пересчёта потенциалов, какие-то из редуцированных весов окажутся отрицательными, что означает, что потенциалы имеют некорректные значения. Однако, это происходит только на промежуточных стадиях, и, при обработке очередных строк на следующих итерациях внутреннего цикла поиска, такие значения выявляются и всегда исправляются. На момент, когда удлиняющий путь найден, все потенциалы пересчитаны и имеют корректные значения. Как так получается, я не представляю.

В этом плане метод кратчайшего пути из книжки куда более прозрачный. Сделал его реализацию в лоб, не задумываясь над производительностью, зато делая упор на визуализацию работы:

Используется синтаксис Java

import java.util.*;

public class Study_Hungarian_4 {
    
//    private static final long seed = 1609857514485L;
    private static final long seed = System .currentTimeMillis ();
    private static final Random rng = new Random (seed);
    
    private static final int width    = 12;
    private static final int rndCount = 3;
    private static final int minCount = 1;
    private static final int height   = 10;
    private static final int maxValue = 50;
    private static int [] [] weights;
    
    private static int [] assignment, matchings;
    private static int [] auxMinima, wayBack;
    private static int [] rowsPotentials, columnsPotentials;
    
    private static boolean [] usedColumns, usedRows;
    
    private static int currentRow, nextColumn;
    
    public static void main (String [] args) {
        
        System .out .println ("Seed " + seed);
        printSeparator ();
        makeRandomTest ();
        diplayWeights ();
        findAssignment ();
        printSeparator ();
        diplayWeights ();
    }
    
    private static void makeRandomTest () {
        int k, l, index;
        int [] countByColumn;
        
        weights    = new int [height] [width];
        assignment = new int [height];
        matchings  = new int          [width];
        Arrays .fill (assignment, -1);
        Arrays .fill (matchings,  -1);
        
        for (k = 0; height > k; ++k) {
            Arrays .fill (weights [k], Integer .MAX_VALUE);
        }
        
        countByColumn = new int [width];
        
        for (k = 0; height > k; ++k) {
            for (l = 0; rndCount > l; ) {
                index = rng .nextInt (width);
                if (Integer .MAX_VALUE != weights [k] [index]) {
                    continue;
                }
                weights [k] [index] = rng .nextInt (maxValue);
                ++countByColumn [index];
                ++l;
            }
            for (l = 0; minCount > l; ++l) {
                index = findMinCountIndex (countByColumn);
                weights [k] [index] = rng .nextInt (maxValue);
                ++countByColumn [index];
            }
        }
    }
    
    private static int findMinCountIndex (int [] countByColumn) {
        int k, count, bestCount, bestIndex;
        
        bestCount = Integer .MAX_VALUE;
        bestIndex = -1;
        
        for (k = 0; width > k; ++k) {
            count = countByColumn [k];
            if (bestCount > count) {
                bestCount = count;
                bestIndex = k;
            }
        }
        
        return bestIndex;
    }
    
    @SuppressWarnings("unused")
    private static void findAssignment () {
        int delta, value, rowIndex, columnIndex, currentColumn;
        
        if (height > width) {
            throw new IllegalArgumentException ("\n\nData height must be less than or equal data width.\n");
        }
        
        rowsPotentials    = new int     [height];
        columnsPotentials = new int     [width];
        auxMinima         = new int     [width];
        wayBack           = new int     [width];
        usedRows          = new boolean [height];
        usedColumns       = new boolean [width];
        
        printSeparator ();
        diplayData ();
        
        for (rowIndex = 0; height > rowIndex; ++rowIndex) {
            
            //      Initialization of new iteration
            
            Arrays .fill (auxMinima,   Integer .MAX_VALUE);
            Arrays .fill (wayBack,     Integer .MAX_VALUE);
            Arrays .fill (usedColumns, false);
            Arrays .fill (usedRows,    false);
            currentRow = rowIndex;
            delta = 0;
            nextColumn = -1;
            
            //      Looking for shortest augmenting path starting with current row
            
            do {
                usedRows [currentRow] = true;
                
                //      Updating list of lengths of searched paths, marking way back
                
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = weights         [currentRow] [columnIndex];
                    if (Integer .MAX_VALUE == value) {
                        continue;
                    }
                    value += delta;
                    value -= rowsPotentials [currentRow]
                           + columnsPotentials           [columnIndex];
                    if (auxMinima [columnIndex] > value) {
                        auxMinima [columnIndex] = value;
                        wayBack   [columnIndex] = currentRow;
                    }
                }
                
                //      Looking for the best unused column and associated path length
                
                delta = Integer .MAX_VALUE;
                
                for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                    if (usedColumns [columnIndex]) {
                        continue;
                    }
                    value = auxMinima [columnIndex];
                    if (delta > value) {
                        delta = value;
                        nextColumn = columnIndex;
                    }
                }
                
                diplayStep ();
                
                if (Integer .MAX_VALUE == delta) {
                    throw new IllegalArgumentException ("\n\nNo assignment is possible.\n");
                }
                
                usedColumns            [nextColumn] = true;
                currentRow = matchings [nextColumn];
                
                //      If the best column is not free, then continue iterations
                
            } while (-1 != currentRow);
            
            //      Recalculating potentials
            
            for (currentRow = 0; rowIndex > currentRow; ++currentRow) {
                if (!usedRows [currentRow]) {
                    continue;
                }
                rowsPotentials [currentRow] += delta - auxMinima [assignment [currentRow]];
            }
            
            rowsPotentials [rowIndex] += delta;
            
            for (columnIndex = 0; width > columnIndex; ++columnIndex) {
                if (!usedColumns [columnIndex]) {
                    continue;
                }
                columnsPotentials [columnIndex] -= delta - auxMinima [columnIndex];
            }
            
            //      Restoring new assignment
            
            do {
                currentRow = wayBack [nextColumn];
                matchings [nextColumn] = currentRow;
                currentColumn = assignment [currentRow];
                assignment [currentRow] = nextColumn;
                nextColumn = currentColumn;
            } while (rowIndex != currentRow);
            
            printSeparator ();
            diplayData ();
        }
    }
    
    private static void diplayWeights () {
        int k, l, m, value;
        
        System .out .println ();
        for (k = 0; height > k; ++k) {
            m = assignment [k];
            for (l = 0; width > l; ++l) {
                value = weights [k] [l];
                if (Integer .MAX_VALUE == value) {
                    if (m == l) {
                        System .out .print (" ####");
                    } else {
                        System .out .print ("   - ");
                    }
                } else {
                    if (m == l) {
                        System .out .print (String .format ("%4s]", "[" + value));
                    } else {
                        System .out .print (String .format ("%4d ", value));
                    }
                }
            }
            System .out .println ();
        }
        System .out .println ();
    }
    
    private static void diplayData () {
        int k, l, m, value;
        
        System .out .println ();
        for (k = 0; height > k; ++k) {
            System .out .print ("#" + k + ((10 > k) ? " " : ""));
            m = assignment [k];
            for (l = 0; width > l; ++l) {
                value = weights [k] [l];
                if (Integer .MAX_VALUE != value) {
                    value -= rowsPotentials [k] + columnsPotentials [l];
                }
                printValue (value, m == l);
            }
            System .out .print ("  ~ ");
            System .out .print (String .format ("%4d ", rowsPotentials [k]));
            System .out .println ();
        }
        System .out .print ("   ");
        for (l = 0; width > l; ++l) {
            System .out .print ("   | ");
        }
        System .out .print ("\n   ");
        for (l = 0; width > l; ++l) {
            System .out .print (String .format ("%4d ", columnsPotentials [l]));
        }
        System .out .println ();
        System .out .println ();
    }
    
    private static void diplayStep () {
        int k;
        
        System .out .print ("#" + currentRow + " row:\n   ");
        for (k = 0; width > k; ++k) {
            if (usedColumns [k]) {
                System .out .print ("   + ");
                continue;
            }
            printValue (usedColumns [k] ? Integer .MAX_VALUE : auxMinima [k], nextColumn == k);
        }
        System .out .print ("\n   ");
        for (k = 0; width > k; ++k) {
            if (usedColumns [k]) {
                System .out .print ("   + ");
                continue;
            }
            printValue (usedColumns [k] ? Integer .MAX_VALUE : wayBack [k], false);
        }
        System .out .println ();
    }
    
    private static void printValue (int value, boolean flag) {
        if (Integer .MAX_VALUE == value) {
            if (flag) {
                System .out .print (" ####");
            } else {
                System .out .print ("   - ");
            }
        } else {
            if (flag) {
                System .out .print (String .format ("%4s]", "[" + value));
            } else {
                System .out .print (String .format ("%4d ", value));
            }
        }
    }
    
    private static void printSeparator () {
        System .out .println ();
        System .out .println ("================================================================================");
    }
}
 

Пример результата работы программы не влез. Как же напрягает этот лимит в 20k символов на сообщение!

Узкое место алгоритма теперь только поиск столбца с наименьшим суммарным весом. Единственный способ ускорить этот процесс, который мне видится, — это использовать какую-нибудь продвинутую структуру данных, которая позволяет добавлять, удалять и модифицировать свои элементы за время $O\left(\log n\right)$, типа PriorityQueue и TreeSet по типу того, как я это делал в соседней теме для поиска в ширину алгоритмом Дэйкстры. Однако тут сразу встаёт вопрос о том, при каких ширинах матрицы весов накладные расходы на поддержание таких структур данных окупятся логарифмической сложностью по сравнению с линейной сложностью решения "в лоб"? Я где-то видел сравнения быстродействия этих двух структур с ArrayList на операциях вставки/удаления элемента в случайном месте. Не смотря на то, что такая операция в ArrayList имеет линейное время выполнения до размеров данных порядка 10k массив со своим $O\left(n\right)$ выигрывал у структур с $O\left(\log n\right)$.

[B@R5uk]

B@R5uk в сообщении #1499145 писал(а):

Однако тут сразу встаёт вопрос о том, при каких ширинах матрицы весов накладные расходы на поддержание таких структур данных окупятся логарифмической сложностью по сравнению с линейной сложностью решения "в лоб"?

Написал программу, проверяющую в режиме, приближенном к боевому, быстродействие реализаций поиска минимума с помощью массива (наивный подход с линейным временем), упорядоченного множества TreeSet и очереди с приоритетом PriorityQueue. Оказалось, что в интересующих меня случаях (ширина рабочего массива до 150) наивный линейный подход лидирует по сравнению со структурами с логарифмическим временем. А ведь его ещё можно усовершенствовать, ускорив как минимум в два раза. Стандартные структуры с логарифмическим временем оказались не очень подходящими для задачи.

При этом на последнем месте (при малых размерах массива) оказалось упорядоченное множество. Видимо, поддержание полной упорядоченности всех элементов является весьма трудоёмкой задачей. Не говоря о том, что модификация элемента требует две операции: предварительное удаление из множества и вставку обратно после модификации. Очередь с приоритетом всегда оказывается немного быстрее упорядоченного множества. Это и понятно: упорядоченность поддерживается только до уровня, необходимого для получения экстремального элемента, нет необходимости упорядочивать всё до самого предела. Однако, очередь не поддерживает эффективную операцию удаления и/или модификации произвольного элемента. Поэтому приходится пихать в очередь элементы по мере их модификации в паре с индексом, а при выделении головы очереди, проверять является ли очередной экстремальный элемент актуальным на данный момент, и, если нет, то отбрасывать его. Это приводит к тому, что размер очереди неконтролируемо растёт и достигает чуть ли не на порядок большей величины, чем размер рабочего массива. В результате — деградация скорости работы, что особенно актуально при небольших размерах рабочего массива (до 100 элементов). Накладные расходы на непрерывное создание новых объектов тоже заметны в диспетчере задач, а ведь этот мусор потом ещё и удалять надо. Подробности этих двух реализаций расписаны на И-Максе в теме про алгоритм Дейкстры поиска пути на графе.

В связи с проделанными исследованиями быстродействия, я пришёл к пониманию того, что мне нужно. Это что-то должно быть массивом величин с произвольным доступом за $O(1)$, и ассоциированной с ним структурой, поддерживающее частичное упорядочивание (для возможности определения экстремального элемента) за время $O(\log n)$. Желательно, чтобы сортирующая структура тоже была реализована внутри массива, так как, когда все рабочие массивы прокэшированы процессором, скорость работы будет максимальна. Фибоначчиева куча по этой причине сразу отпадает. Я делал выбор между деревом отрезков и двоичной кучей (возможно ещё что-то существует?), выбор пал на двоичную кучу, так как она компактнее по размерам и не поддерживает излишний функционал.

Реализация содержит три массива: массив величин, массив-кучу индексов этих величин и массив индексов индексов в куче. То есть, в куче хранятся не сами значения, а их индексы в массиве значений. Третий массив требуется процедурами добавления/удаления/модификации элемента: чтобы быстро находить соответствующие индексы элементов в куче в процессе восстановления её свойства "кучевости". Таким образом, за время $O(1)$ можно проверить по индексу наличие инициализированного элемента в массиве, прочитать значение этого элемента, узнать положение его индекса в куче. За время $O(\log n)$ производится удаление/добавление/модификация элемента массива. При этом в вики пишут (со ссылкой на авторитетные источники), что это худший случай. В среднем для случайных куч операция добавления случайного элемента делается за время $O(1)$, что, разумеется, не может не радовать.

Для проверки работоспособности моего подхода с двоичной кучей сделал вот такую вот программку с визуализацией:

Используется синтаксис Java

import java.util.*;

public class Study_BinaryHeap {
    
    private static final long seed = System .currentTimeMillis ();
    private static final Random rng = new Random (seed);
    
    private static final int size = 12;
    private static final int [] values = new int [size];
    private static final int [] heapIndices = new int [size];
    private static final int [] heapReverse = new int [size];
    private static int heapSize;
    
    public static void main (String [] args) {
        int k, l;
        
        heapInit ();
        
        for (k = 0; 6 > k; ++k) {
            for (l = 0; 4 > l; ++l) {
                setElement (rng .nextInt (size), rng .nextInt (50));
                display ();
            }
            removeHead ();
            display ();
        }
        while (0 < heapSize) {
            removeHead ();
            display ();
        }
    }
    
    private static void heapInit () {
        
        System .out .println ("Seed: " + seed);
        System .out .println ();
        Arrays .fill (heapIndices, -1);
        heapSize = 0;
    }
    
    private static void setElement (int index, int value) {
        
        System .out .println ("Setting [" + index + "] to " + value);
        
        if (-1 == heapIndices [index]) {
            values [index] = value;
            bubbleUp (index, heapSize);
            ++heapSize;
            return;
        }
        if (values [index] > value) {
            values [index] = value;
            bubbleUp (index, heapIndices [index]);
            return;
        }
        if (values [index] < value) {
            values [index] = value;
            sinkDown (index, heapIndices [index]);
        }
    }
    
    private static void removeHead () {
        
        System .out .println ("Removing head " + values [heapReverse [0]] + " at [" + heapReverse [0] + "]");
        
        --heapSize;
        heapIndices [heapReverse [0]] = -1;
        sinkDown (heapReverse [heapSize], 0);
    }
    
    private static void bubbleUp (int index, int heapIndex) {
        int value, parentIndex, parentReverse;
        
        value = values [index];
        while (0 < heapIndex) {
            parentIndex = (heapIndex - 1) / 2;
            parentReverse = heapReverse [parentIndex];
            if (value >= values [parentReverse]) {
                break;
            }
            heapReverse [heapIndex] = parentReverse;
            heapIndices [parentReverse] = heapIndex;
            heapIndex = parentIndex;
        }
        heapReverse [heapIndex] = index;
        heapIndices [index] = heapIndex;
    }
    
    private static void sinkDown (int index, int heapIndex) {
        int value, bestIndex, childIndex, bestReverse, childReverse, bestValue;
        
        value = values [index];
        bestReverse = -1;
        while (true) {
            bestValue = value;
            bestIndex = heapIndex;
            childIndex = 2 * heapIndex + 1;
            if (heapSize > childIndex) {
                childReverse = heapReverse [childIndex];
                if (bestValue > values [childReverse]) {
                    bestValue = values [childReverse];
                    bestIndex = childIndex;
                    bestReverse = childReverse;
                }
            }
            ++childIndex;
            if (heapSize > childIndex) {
                childReverse = heapReverse [childIndex];
                if (bestValue > values [childReverse]) {
                    bestIndex = childIndex;
                    bestReverse = childReverse;
                }
            }
            if (heapIndex == bestIndex) {
                break;
            }
            heapReverse [heapIndex] = bestReverse;
            heapIndices [bestReverse] = heapIndex;
            heapIndex = bestIndex;
        }
        heapReverse [heapIndex] = index;
        heapIndices [index] = heapIndex;
    }
    
    private static void display () {
        int k;
        
        System .out .println ();
        for (k = 0; size > k; ++k) {
            System .out .print (String .format ("%4d", k));
        }
        System .out .print ("  NN\n");
        for (k = 0; size > k; ++k) {
            if (-1 == heapIndices [k]) {
                System .out .print ("   -");
            } else {
                System .out .print (String .format ("%4d", values [k]));
            }
        }
        System .out .print ("  Values\n");
        for (k = 0; size > k; ++k) {
            if (-1 == heapIndices [k]) {
                System .out .print ("   -");
            } else {
                System .out .print (String .format ("%4d", heapIndices [k]));
            }
        }
        System .out .print ("  Indices in heap\n");
        for (k = 0; size > k; ++k) {
            if (heapSize > k) {
                System .out .print (String .format ("%4d", heapReverse [k]));
            } else {
                System .out .print ("    ");
            }
        }
        System .out .print ("  Heap of indices\n");
        for (k = 0; size > k; ++k) {
            System .out .print ("====");
        }
        System .out .print ("=================\n");
    }
}
 

Результаты работы выглядят примерно так:

Используется синтаксис Text

Seed: 1610039554445

Setting [5] to 23

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -  23   -   -   -   -   -   -  Values
   -   -   -   -   -   0   -   -   -   -   -   -  Indices in heap
   5                                              Heap of indices
====================
Setting [5] to 1

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -   1   -   -   -   -   -   -  Values
   -   -   -   -   -   0   -   -   -   -   -   -  Indices in heap
   5                                              Heap of indices
====================
Setting [7] to 1

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -   1   -   1   -   -   -   -  Values
   -   -   -   -   -   0   -   1   -   -   -   -  Indices in heap
   5   7                                          Heap of indices
====================
Setting [8] to 37

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -   1   -   1  37   -   -   -  Values
   -   -   -   -   -   0   -   1   2   -   -   -  Indices in heap
   5   7   8                                      Heap of indices
====================
Removing head 1 at [5]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -   -   -   1  37   -   -   -  Values
   -   -   -   -   -   -   -   0   1   -   -   -  Indices in heap
   7   8                                          Heap of indices
====================
Setting [5] to 34

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -  34   -   1  37   -   -   -  Values
   -   -   -   -   -   2   -   0   1   -   -   -  Indices in heap
   7   8   5                                      Heap of indices
====================
Setting [11] to 23

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -  34   -   1  37   -   -  23  Values
   -   -   -   -   -   2   -   0   3   -   -   1  Indices in heap
   7  11   5   8                                  Heap of indices
====================
Setting [0] to 18

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  18   -   -   -   -  34   -   1  37   -   -  23  Values
   1   -   -   -   -   2   -   0   3   -   -   4  Indices in heap
   7   0   5   8  11                              Heap of indices
====================
Setting [0] to 38

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -   -   -  34   -   1  37   -   -  23  Values
   4   -   -   -   -   2   -   0   3   -   -   1  Indices in heap
   7  11   5   8   0                              Heap of indices
====================
Removing head 1 at [7]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -   -   -  34   -   -  37   -   -  23  Values
   3   -   -   -   -   2   -   -   1   -   -   0  Indices in heap
  11   8   5   0                                  Heap of indices
====================
Setting [3] to 24

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -  24   -  34   -   -  37   -   -  23  Values
   3   -   -   1   -   2   -   -   4   -   -   0  Indices in heap
  11   3   5   0   8                              Heap of indices
====================
Setting [10] to 17

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -  24   -  34   -   -  37   -  17  23  Values
   3   -   -   1   -   5   -   -   4   -   0   2  Indices in heap
  10   3  11   0   8   5                          Heap of indices
====================
Setting [3] to 12

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -  12   -  34   -   -  37   -  17  23  Values
   3   -   -   0   -   5   -   -   4   -   1   2  Indices in heap
   3  10  11   0   8   5                          Heap of indices
====================
Setting [9] to 23

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -  12   -  34   -   -  37  23  17  23  Values
   3   -   -   0   -   5   -   -   4   6   1   2  Indices in heap
   3  10  11   0   8   5   9                      Heap of indices
====================
Removing head 12 at [3]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -   -   -  34   -   -  37  23  17  23  Values
   3   -   -   -   -   5   -   -   4   1   0   2  Indices in heap
  10   9  11   0   8   5                          Heap of indices
====================
Setting [9] to 26

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -   -   -  34   -   -  37  26  17  23  Values
   3   -   -   -   -   5   -   -   4   1   0   2  Indices in heap
  10   9  11   0   8   5                          Heap of indices
====================
Setting [8] to 47

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  38   -   -   -   -  34   -   -  47  26  17  23  Values
   3   -   -   -   -   5   -   -   4   1   0   2  Indices in heap
  10   9  11   0   8   5                          Heap of indices
====================
Setting [0] to 21

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  21   -   -   -   -  34   -   -  47  26  17  23  Values
   1   -   -   -   -   5   -   -   4   3   0   2  Indices in heap
  10   0  11   9   8   5                          Heap of indices
====================
Setting [10] to 43

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  21   -   -   -   -  34   -   -  47  26  43  23  Values
   0   -   -   -   -   5   -   -   4   1   3   2  Indices in heap
   0   9  11  10   8   5                          Heap of indices
====================
Removing head 21 at [0]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -   -  34   -   -  47  26  43  23  Values
   -   -   -   -   -   2   -   -   4   1   3   0  Indices in heap
  11   9   5  10   8                              Heap of indices
====================
Setting [4] to 47

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -  47  34   -   -  47  26  43  23  Values
   -   -   -   -   5   2   -   -   4   1   3   0  Indices in heap
  11   9   5  10   8   4                          Heap of indices
====================
Setting [7] to 19

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -  47  34   -  19  47  26  43  23  Values
   -   -   -   -   5   6   -   0   4   1   3   2  Indices in heap
   7   9  11  10   8   4   5                      Heap of indices
====================
Setting [9] to 19

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -  47  34   -  19  47  19  43  23  Values
   -   -   -   -   5   6   -   0   4   1   3   2  Indices in heap
   7   9  11  10   8   4   5                      Heap of indices
====================
Setting [8] to 26

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -  47  34   -  19  26  19  43  23  Values
   -   -   -   -   5   6   -   0   4   1   3   2  Indices in heap
   7   9  11  10   8   4   5                      Heap of indices
====================
Removing head 19 at [7]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   -   -   -   -  47  34   -   -  26  19  43  23  Values
   -   -   -   -   5   4   -   -   1   0   3   2  Indices in heap
   9   8  11  10   5   4                          Heap of indices
====================
Setting [0] to 3

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   3   -   -   -  47  34   -   -  26  19  43  23  Values
   0   -   -   -   5   4   -   -   1   2   3   6  Indices in heap
   0   8   9  10   5   4  11                      Heap of indices
====================
Setting [5] to 2

   0   1   2   3   4   5   6   7   8   9  10  11  NN
   3   -   -   -  47   2   -   -  26  19  43  23  Values
   1   -   -   -   5   0   -   -   4   2   3   6  Indices in heap
   5   0   9  10   8   4  11                      Heap of indices
====================
Setting [0] to 48

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  47   2   -   -  26  19  43  23  Values
   4   -   -   -   5   0   -   -   1   2   3   6  Indices in heap
   5   8   9  10   0   4  11                      Heap of indices
====================
Setting [4] to 46

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   2   -   -  26  19  43  23  Values
   4   -   -   -   5   0   -   -   1   2   3   6  Indices in heap
   5   8   9  10   0   4  11                      Heap of indices
====================
Removing head 2 at [5]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   -   -   -  26  19  43  23  Values
   4   -   -   -   5   -   -   -   1   0   3   2  Indices in heap
   9   8  11  10   0   4                          Heap of indices
====================
Removing head 19 at [9]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   -   -   -  26   -  43  23  Values
   4   -   -   -   2   -   -   -   1   -   3   0  Indices in heap
  11   8   4  10   0                              Heap of indices
====================
Removing head 23 at [11]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   -   -   -  26   -  43   -  Values
   3   -   -   -   2   -   -   -   0   -   1   -  Indices in heap
   8  10   4   0                                  Heap of indices
====================
Removing head 26 at [8]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   -   -   -   -   -  43   -  Values
   1   -   -   -   2   -   -   -   -   -   0   -  Indices in heap
  10   0   4                                      Heap of indices
====================
Removing head 43 at [10]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -  46   -   -   -   -   -   -   -  Values
   1   -   -   -   0   -   -   -   -   -   -   -  Indices in heap
   4   0                                          Heap of indices
====================
Removing head 46 at [4]

   0   1   2   3   4   5   6   7   8   9  10  11  NN
  48   -   -   -   -   -   -   -   -   -   -   -  Values
   0   -   -   -   -   -   -   -   -   -   -   -  Indices in heap
   0                                              Heap of indices
====================
Removing head 48 at [0]
 

Осталось убедится, что нигде нет ошибок и загнать код в программу для боевого тестирования для сравнения с остальными реализациями. Я сильно огорчусь, если этот новый метод не выйдет в лидеры.