Навеяно темой
topic142399.html, я решил конкретизировать вопрос

Пусть у нас есть последовательность

, где

без потери общности можно считать целым. Требуется по

последовательным членам
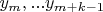
найти

Для случая

получим формулу (для удобства обозначим

за

)

, если теперь выразить

, получим формулу
Otta из темы.
Для

будет

и т.д.
Интересно, что если у нас все

, и мы хотим выразить определенную степень через соседние степени без операций извлечения корня, то нужно взять определенное количество соседних степеней в зависимости показателя степени.
Участники просто не поняли условие задачи




