Итак, чтобы поменять знак в выражении, нужно либо умножить все выражение на -1, либо поменять местами значения в скобках. Результат будет одинаковый.
Не будет:

, как и
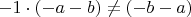
.
Надо именно домножить скобку на

, после чего упростить выражение (например внести

в скобку, домножив каждое слагаемое в скобке на

и при желании переставив слагаемые (а не вычитаемые!) местами).
-- 10.10.2020, 23:53 --Кроме того, произведение в выражении

можно спутать с записью функции

, а тогда домножение её на

конечно правильно, но может не привести к смене знаков в скобках (например для чётных функций). Поэтому стоило бы уточнить что выражение слева это именно запись произведения, а не функции.