Полёт по радиусу в поле r^-2

[nnosipov]

Утундрий в сообщении #1459310 писал(а):

А зачем? Мапля выдала, значит истина.

Вот, кстати, реальный случай. Несколько лет назад мой студент решал такую задачу:

$$y''=-\frac{C}{y^2}, \quad y'(0)=R>0, \quad y'(0)=0.$$

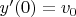
Здесь $C>0$, это важно. Несмотря на все мои увещевания, что, дескать, задача решается простым интегрированием, он засунул ее в Maple и действительно получил какую-то хрень, с которой так и не смог разобраться. Между тем, еще раньше мы со школьником решали эту задачу (и даже в более общей постановке, где $y'(0)=v_0$) обычным человеческим образом и проблем не испытали. Кстати, конечный результат интегрирования в задаче такой:

$$t(y)=\sqrt{\frac{R}{2C}}\left(R\arccos{\sqrt{\frac{y}{R}}}+\sqrt{y(R-y)}\right).$$

(Разумеется, обратная зависимость $y=y(t)$ будет неэлементарной, но это более чем ожидалось.) Соответственно, "время падения" получалось таким:

$$T=t(0)=\frac{\pi\sqrt{2}}{4}\frac{R^{3/2}}{\sqrt{C}}.$$

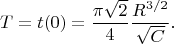
Очевидно, в случае $C<0$ вместо обычного арккосинуса будет гиперболический. В любом случае, это хорошая учебная задача, которую можно давать и школьникам, и студентам (последним --- чтобы объяснить, что иногда полезно что-то делать просто руками и не доверяться железкам на 100%).

-- Пт май 01, 2020 13:06:47 --

Pphantom в сообщении #1459276 писал(а):

Скачиваем эту книжку
и читаем пункт 1.6 (можно вместе с окрестностями).

Мне кажется, здесь какая-то более сложная (и серьезная, "для взрослых") задача решается.

[pogulyat_vyshel]

а накой это вообще надо выписывать квадратуры в этой и в подобных задачах? для качественного анализа движения квадратуры не нужны, мешают только, а если надо количественные результаты, траекторию просчитать на каком-то отрезке, то для этого существует Рунге-Кутт а не программы символьных вычислений

[nnosipov]

pogulyat_vyshel в сообщении #1459330 писал(а):

для качественного анализа движения квадратуры не нужны, мешают только

То есть они вредны? (Непонятно, в чем может быть принципиальный вред простой явной формулы.) А зачем тогда студентов учат их находить? Или уже не учат? Меня вот учили (по задачнику Филиппова), да и pogulyat_vyshel вряд ли этого избежал. Было бы интересно услышать комментарий Red_Herring по этому поводу.

Символьному интегрированию в системах компьютерной алгебры уделяется приличное место. Неужели это никому не нужно? Как-то не верится.

[Red_Herring]

pogulyat_vyshel в сообщении #1459330 писал(а):

а накой это вообще надо выписывать квадратуры в этой и в подобных задачах? для качественного анализа движения квадратуры не нужны, мешают только, а если надо количественные результаты, траекторию просчитать на каком-то отрезке, то для этого существует Рунге-Кутт а не программы символьных вычислений

В принципе--да, но вот в чуть более общей задаче, а именно при движении в таком поле с ненулевым угловым моментом, интегрируя в полярных координатах мы получим движение по гиперболе. Правда, в отличие от притягивающегоо потенциала $0$ будет находиться в "другом" ее фокусе. Т.ч. квадратуры не всегда дурацкие

[nnosipov]

Red_Herring в сообщении #1459353 писал(а):

мы получим движение по гиперболе

А что, парабола невозможна?

[Geen]

nnosipov в сообщении #1459358 писал(а):

Red_Herring в сообщении #1459353 писал(а):

мы получим движение по гиперболе

А что, парабола невозможна?

При отталкивании??

[nnosipov]

Geen в сообщении #1459360 писал(а):

При отталкивании??

Да, при отталкивании. (Я не знаю ответ, просто спрашиваю.)

[Red_Herring]

Ну ответ будет $r= \frac{1}{A+B\cos(\theta)}$ (после поворота), но при притягивании $A>0$ (и тогда мы получаем э,п,г при $A>|B|, A=|B|, A<|B|$ соответственно, а при отталкивании $A<0$ и все однозначно: $|A|\le |B|$... и в случае равенства будет радиальное двиижение

[nnosipov]

Red_Herring в сообщении #1459364 писал(а):

в случае равенства будет радиальное двиижение

Спасибо. А вообще, хорошая задача для медитации.

[pogulyat_vyshel]

Red_Herring в сообщении #1459353 писал(а):

т в чуть более общей задаче, а именно при движении в таком поле с ненулевым угловым моментом, интегрируя в полярных координатах мы получим движение по гиперболе.

да получим из формул Бине ("Механика" Вильке), квадратуры с плюс-минус интегралами от диких алгебраических функций не понадобятся и здесь

[Pphantom]

(Оффтоп)

nnosipov в сообщении #1459328 писал(а):

Мне кажется, здесь какая-то более сложная (и серьезная, "для взрослых") задача решается.

Ну, ТС хотел "другие способы"...

[Alex_J]

Утундрий в сообщении #1459310 писал(а):

Я практически уверен, что ТС не проверял своё "решение" подстановкой его в уравнение

(Оффтоп)

Печально, что "Мапля" при повторной постановке задачи так и не выдала первоначальный вариант, как я ни проверял на возможные опечатки при вводе в первый раз. Проверку решение, к сожалению, не прошло, ошибка найдена ))

nnosipov в сообщении #1459328 писал(а):

(Разумеется, обратная зависимость $y=y(t)$ будет неэлементарной, но это более чем ожидалось.)

Об этом и речь. Вопрос топика был как раз в том, есть ли иные пути, совершенно верно. И другие решения. Но логика и интуиция подсказывает, что решение должно быть одно (т.е. решения на основе "диких" функций и кеплеровские должны совпадать).

[g______d]

pogulyat_vyshel в сообщении #1459330 писал(а):

а накой это вообще надо выписывать квадратуры в этой и в подобных задачах?

Точно не знаю, но подозреваю, что если рассмотреть малое возмущение этой задачи (например, третьим телом) и решать методами теории возмущений (малые знаменатели, КАМ), может потребоваться нетривиальная информация о решениях невозмущённой задачи.

nnosipov в сообщении #1459328 писал(а):

Разумеется, обратная зависимость $y=y(t)$ будет неэлементарной, но это более чем ожидалось.

Как выяснилось, это частный случай уравнения Кеплера (я до этого не знал названия).

https://en.wikipedia.org/wiki/Kepler%27s_equation

Что более забавно -- оно очень похоже на уравнение циклоиды. Судя по всему, это обнаружил Кристофер Рен, но в исторические детали я не вдавался.

https://www.jstor.org/stable/3519869?seq=1

[nnosipov]

g______d
Спасибо за ссылки. Оказывается, есть отдельная статья https://en.wikipedia.org/wiki/Radial_trajectory В общем, люди как-то не стесняются писать явные формулы.

Ну и все-таки, надо студентов учить брать квадратуры или ну его на фиг? Четкого ответа как-то не прозвучало.

[pogulyat_vyshel]

nnosipov в сообщении #1459487 писал(а):

Четкого ответа как-то не прозвучало.

хорошо, сейчас прозвучит

nnosipov в сообщении #1459348 писал(а):

Непонятно, в чем может быть принципиальный вред простой явной формулы.

в том, что студент ее выписывает и думает, что решил задачу. К сожалению, многие преподаватели дифуров очень этому заблуждению способствуют

nnosipov в сообщении #1459348 писал(а):

А зачем тогда студентов учат их находить?

Потому, что они бывают полезны в ряде вопросов. Специальных вопросов (в частности то о чем говорил g______d ). При качественном исследовании динамики интегрируемой задачи они бесполезны за исключением, возможно, простейших случаев типа гармонического осциллятора. Уже в случае математического маятника рисование фазового портрета на основе графика потенциальной энергии несоизмеримо удобней разглядывания квадратур.