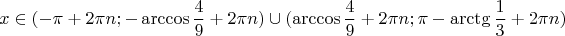Cheloveck, попробую показать, как я решал бы Вашу задачу.
1. Так как период котангенса всего-навсего

, на окружности неравенству с котангенсом будут соответствовать сразу две дуги (о чём Вам говорит
gris). Поэтому начнём с "более сложного" - с изображения решения неравенства

. Отмечаем на окружности точки, где котангенс равен

(и, значит, тангенс равен

). Это точка

и
диаметрально противоположная ей - точка

. Кроме того, отмечаем точки, в которых котангенс не существует - точки

и

(обозначения этих точек потом, возможно, придётся поправить; пока пусть будет так). Получаем первую картинку:
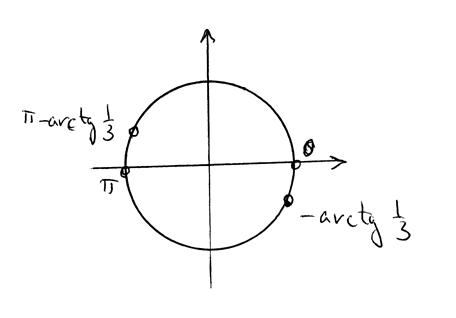 2.
2. Теперь, учитывая, что котангенс - функция убывающая, делаем вывод, что для решения неравенства

нам нужно выбрать значения аргумента меньшие чем

(на верхней дуге). Таким образом, выбираем интервал

на верхней дуге, отмечаем его штриховкой. Мысленно поворачиваем его на

и добавляем штриховку на аналогичный фрагмент нижней полуокружности - получаем вторую картинку:
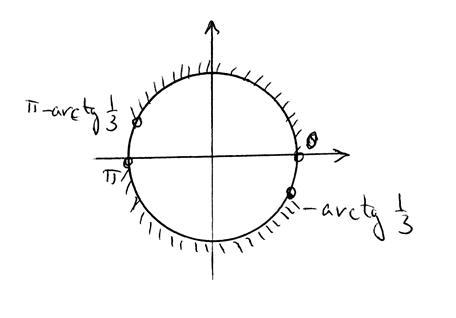 3.
3. Теперь пришло время учесть неравенство с косинусом. Проводим вертикальную прямую, которая рассечёт окружность в точках, соответствующих значениям косинуса

, то есть в точках
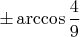
, выбираем часть окружности слева от этой прямой - см. третью картинку:
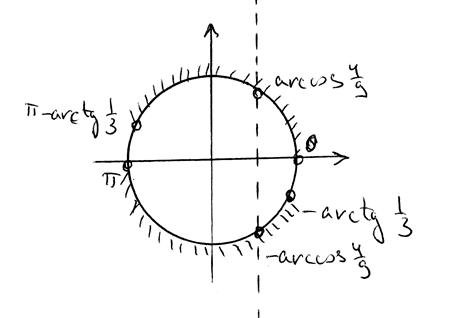 4.
4. Прежде чем выписывать ответ, проверим корректность наших обозначений на рисунке. Легко заметить, что точку, которую мы первоначально обозначили как

, следует переобозначить как

(чтобы
при возрастании аргумента мы дошли до значения

). Дорисовываем там где надо знак "минус":
 5.
5. Можно начинать выписывать ответ. Нам нужно включить в ответ лишь те фрагменты заштрихованных дуг, которые расположены левее нашей вертикальной прямой. Записываем:
 6.
6. Чтобы получить полный ответ, учитываем периодичность (добавляем ко всем точкам

):