Есть следующая задача.
Требуется: Составить алгоритм имитационного моделирования излучения и поглощения фотона для одномерного случая. В момент времени:
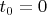
- фотон излучается свободным атомом в точке:

. Дискрет моделирования по

выбрать так, чтобы вероятность обнаружения фотона в момент времени

в дискрете

стремилась к

. Шаг моделирования по

выбрать так, чтобы на каждом следующем шаге моделирования фотон находился в каждом следующем дискрете по направлению распространения. Детекторы фотонов:

,

,

- расположены в точках с координатами:

;

;

. Вероятность обнаружения фотона каждым из детекторов:

. При попадании в детектор фотон поглощается. Провести моделирование и определить вероятность попадания фотона в каждый из детекторов.
Если я правильно понимаю - в момент излучения фотон в данной задаче находится в суперпозиции двух направлений распространения, поэтому волновая функция его положения в любой из моментов времени может быть записана как:

где

- волновая функция положения фотона для отрицательного направления распространения,

- волновая функция положения фотона для положительного направления распространения, а

и

- постоянные коэффициенты.
Тогда эквивалентная схема моделируемого эксперимента в момент времени:

- будет выглядеть так:

Причём, амплитуды для излучения фотона в обе стороны совпадают, поэтому:

Исходя из определения волновой функции положения фотона, как амплитуды вероятности обнаружения фотона в соответствующем положении, алгоритм имитационного моделирования должен быть (насколько я понимаю) примерно следующим:
1. Выполнить приращение времени.
2. Вычислить волновые функции

и

для данного момента времени.
3. Рассчитать вероятности обнаружения фотона в каждом из детекторов.
4. Если вероятность обнаружения фотона отличается от нуля для двух детекторов - выбрать (с учётом нормировки) один из детекторов, в качестве обнаружившего фотон.
5. При обнаружении фотона в одном из детекторов - учесть "попадание" для итоговой статистики этого детектора и завершить моделирование.
6. Перейти к пункту 1.
Но при таком алгоритме имитационное моделирование даёт следующую итоговую статистику "попаданий":



Правильные же результаты должны быть:



Понятно, что фотон не может пройти в положительном направлении дальше детектора

и вне зависимости от факта обнаружения фотона в детекторе

- волновая функция

должна уничтожаться в момент времени

:

и в случае, если фотон не был обнаружен в детекторе

, то в момент времени

волновая функция положения фотона уже будет иметь вид:


причём

Но какое условие должно использоваться в таком случае в алгоритме имитационного моделирования для определения того момента времени, когда волновая функция должна измениться?