If we do not want the rawscore for a node exceed a certain value R we can ask for the number the number

of the "good nodes" which have this property. Surprisingly there is a quite simple fomula which gives an excellent approximation for

.
For the calculation we do not work with products of the prime numbers but with the sums of their natural logarithms. For problem size N a node consists of N-1 of the N(N-1)/2:=M primes, so there are Binomial(M,N-1) different nodes. The energy E(n) of a node n then is the sum of the logarithms of all primes of this node in this logarithmic representation. We define all nodes to have the same probability and in this way E(n) is a random variable in the space of all nodes. We want to know more about the probability distribution of E.
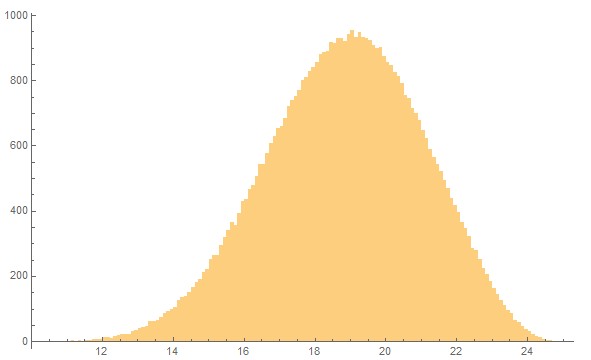
Here is a look at the distribution for N=7 with M= 21 and Binomial(21,6) = 54264 nodes. The bin size of the histogram is 0.1.
I is not difficult to show that the the mean value
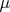
is exactly

,
which for example is 18.8219 for N=7.
This also is the target energy for a node in the logarithmic representation,

is the target energy for a node in the usual representation.
The variance

can be shown to be exactly
![$\sigma^2 = \frac{2}{N(N^2-1)} \sum\limits_{i=1}^{M}[(N-1)Log(Prime(i))-\mu]^2$ $\sigma^2 = \frac{2}{N(N^2-1)} \sum\limits_{i=1}^{M}[(N-1)Log(Prime(i))-\mu]^2$](https://dxdy-01.korotkov.co.uk/f/4/e/1/4e1c40eb32470a66b907a4223eaf668582.png)
.
Already for N=7 the graph shows a good approximation to a Gaussian distribution. This is a consequence of the central limit theorem. With the formula for this distribution (
https://en.wikipedia.org/wiki/Normal_distribution)we can approximate the number

of good nodes in a small interval
![$ [\mu-\epsilon,\mu+\epsilon] $ $ [\mu-\epsilon,\mu+\epsilon] $](https://dxdy-01.korotkov.co.uk/f/0/3/c/03c9f1dd99ab7d204a2c6a547e6baaa782.png)
around the mean value:

I also can show that we have to choose

for all nodes which should contribute with no higher value than R to the total rawscore. If we choose for R the "Best Raw Score" in Al's table we count all nodes which could be candidates for a solution. So finally we get for the number of good nodes

For N in [4..28] we have

{5.15, 9.04, 13.7, 18.8, 24.4, 30.4, 36.7, 43.2, 50.0, 57.0, 64.3, 71.7, 79.2, 87.0, 94.8, 103., 111., 119., 128., 136., 145., 153., 162., 171., 180.}

{0.896, 1.39, 1.83, 2.21, 2.54, 2.84, 3.11, 3.36, 3.58, 3.80, 4.00, 4.19, 4.37, 4.53, 4.70, 4.85, 5.00, 5.14, 5.28, 5.42, 5.54, 5.67, 5.79, 5.91, 6.03}
and from this with the current best Raw Scores we get

{9, 19, 32, 70, 683, 1073, 5274, 11985, 47345, 216334., 1.817*10^6, 2.352*10^7, 2.778*10^8, 3.823*10^9, 7.209*10^10, 1.432*10^12, 2.42*10^13, 8.321*10^14, 1.314*10^16, 2.369*10^17, 6.696*10^18, 2.036*10^20, 1.869*10^22, 6.952*10^23, 1.353*10^25}
Since I generated the good nodes for N= 4 to 13 with my program we can compare this with the real number of good nodes:

{10, 17, 30, 68, 619, 1002, 5114, 11589, 45758, 210322}
The approximation seems to be very good and the quality increases with higher N.