Пусть

- некоторая конечная дробь. Что можно сказать о бесконечной дроби с соответствующим чистым периодом? Запишем уравнение:

или так:

Из последней записи видно, что

-ый остаток дроби

равен самому

, то есть

Отсюда

И поскольку

, получаем окончательно

(комментарий 2)
Основание квадрата под радикалом в выражении (14) достойно отдельного рассмотрения:  суть cумма элементов пары подх. дробей, расположенных по диагонали. Выделим это в отдельную функцию
суть cумма элементов пары подх. дробей, расположенных по диагонали. Выделим это в отдельную функцию  и запишем в континуантах:
и запишем в континуантах:![$$\left \{ a_1,a_2,…a_{n-1},a_n\right \}=[a_1,a_2,…a_{n-1},a_n]+[a_2,…a_{n-1}]=$$ $$\left \{ a_1,a_2,…a_{n-1},a_n\right \}=[a_1,a_2,…a_{n-1},a_n]+[a_2,…a_{n-1}]=$$](https://dxdy-04.korotkov.co.uk/f/b/6/b/b6bf75e87006d42035667692ce20828882.png)
![$$a_n[a_1,a_2,…,a_{n-2},a_{n-1}]+[a_1,a_2,…a_{n-2}]+[a_2,…,a_{n-2},a_{n-1}]=$$ $$a_n[a_1,a_2,…,a_{n-2},a_{n-1}]+[a_1,a_2,…a_{n-2}]+[a_2,…,a_{n-2},a_{n-1}]=$$](https://dxdy-04.korotkov.co.uk/f/b/a/7/ba74c6cc08e3f552941599fa779e7ec582.png)
![$$[a_n,a_1,a_2,…,a_{n-2},a_{n-1}]+[a_1,a_2,…,a_{n-2}]=\left \{ a_n,a_1,a_2,…,a_{n-2},a_{n-1}\right \}=$$ $$[a_n,a_1,a_2,…,a_{n-2},a_{n-1}]+[a_1,a_2,…,a_{n-2}]=\left \{ a_n,a_1,a_2,…,a_{n-2},a_{n-1}\right \}=$$](https://dxdy-01.korotkov.co.uk/f/0/3/b/03bce58dfcc1b013c5e8b1291bc9dc6582.png)
 Иными словами, для такой супер-K по меткому выражению одного хорошего математика применимо правило «круглого стола», когда невозможно указать из гостей на первого или последнего. На бумаге «кольцевать» последовательности не удобно, но для строчной записи можно дать следующую формулировку: правило обратного движения (1) справедливо не только для всей последовательности знаков супер-K, но и для двух участков ее произвольного разбиения:
Иными словами, для такой супер-K по меткому выражению одного хорошего математика применимо правило «круглого стола», когда невозможно указать из гостей на первого или последнего. На бумаге «кольцевать» последовательности не удобно, но для строчной записи можно дать следующую формулировку: правило обратного движения (1) справедливо не только для всей последовательности знаков супер-K, но и для двух участков ее произвольного разбиения: Правило нуля внутри последовательности остается в силе, по краям же ноль не исчезает:
Правило нуля внутри последовательности остается в силе, по краям же ноль не исчезает:![$$\left \{0,a_1,a_2,…a_{n-1},a_n \right \}=\left \{a_1,a_2,…a_{n-1},a_n,0\right \}=[a_1,a_2,…a_{n-1}]+[a_2,…a_{n-1},a_n]\ -$$ $$\left \{0,a_1,a_2,…a_{n-1},a_n \right \}=\left \{a_1,a_2,…a_{n-1},a_n,0\right \}=[a_1,a_2,…a_{n-1}]+[a_2,…a_{n-1},a_n]\ -$$](https://dxdy-02.korotkov.co.uk/f/5/a/3/5a301066d7e819e091e9fbe15feddc3b82.png) суть сумма элементов пары подх. дробей, расположенных по другой диагонали. Верно также
суть сумма элементов пары подх. дробей, расположенных по другой диагонали. Верно также![$$[a_1,a_2,…a_{n-1},a_n]-[a_2,…a_{n-1}]=\left \{ 1,(a_1-1),a_2,…a_{n-1},(a_n-1) \right \}$$ $$[a_1,a_2,…a_{n-1},a_n]-[a_2,…a_{n-1}]=\left \{ 1,(a_1-1),a_2,…a_{n-1},(a_n-1) \right \}$$](https://dxdy-01.korotkov.co.uk/f/0/f/d/0fdb8b65a7c26672c8e777923220644282.png) Выражение (14) можно тогда переписать так:
Выражение (14) можно тогда переписать так:![$$(a_1,a_2,…a_{n-1},a_n)=\dfrac{\left \{ 1,(a_1-1),a_2,…a_{n-1},(a_n-1)\right \}+\sqrt{\left \{ a_1,a_2,…a_{n-1},a_n \right \}^2-4\cdot(-1)^n}}{2[a_2,…a_{n-1},a_n]}$$ $$(a_1,a_2,…a_{n-1},a_n)=\dfrac{\left \{ 1,(a_1-1),a_2,…a_{n-1},(a_n-1)\right \}+\sqrt{\left \{ a_1,a_2,…a_{n-1},a_n \right \}^2-4\cdot(-1)^n}}{2[a_2,…a_{n-1},a_n]}$$](https://dxdy-04.korotkov.co.uk/f/3/3/0/330f7b84b70aa8a844699b55eaecd67d82.png) и для всех круговых перестановок значение под радикалом остается неизменным. Это свойство объясняется еще справедливостью определения Эйлера в отношении супер-K как суммы одночленов, образованных вычеркиванием всех возможных пар соседних элементов из одночлена
и для всех круговых перестановок значение под радикалом остается неизменным. Это свойство объясняется еще справедливостью определения Эйлера в отношении супер-K как суммы одночленов, образованных вычеркиванием всех возможных пар соседних элементов из одночлена  если элементы расположены не в строку, как в случае континуант, а в «замкнутую строку», причем одночлен со всеми вычеркнутыми парами при четном количестве знаков имеет значение не 1, а 2. Получить алгоритмически последовательность супер-K для натурального аргумента или установить тождественную связь
если элементы расположены не в строку, как в случае континуант, а в «замкнутую строку», причем одночлен со всеми вычеркнутыми парами при четном количестве знаков имеет значение не 1, а 2. Получить алгоритмически последовательность супер-K для натурального аргумента или установить тождественную связь ![$[a_1,a_2,…a_{n-1},a_n]=\left \{ x_1,x_2,…x_{m-1},x_m \right \}$ $[a_1,a_2,…a_{n-1},a_n]=\left \{ x_1,x_2,…x_{m-1},x_m \right \}$](https://dxdy-01.korotkov.co.uk/f/c/9/0/c90c47185ab0ca2591a17fa3c6297b5082.png) в общем виде не удалось. С палиндромами как всегда легче:
в общем виде не удалось. С палиндромами как всегда легче:![$$[a_1,a_2,…a_2,a_1]=\left \{ (a_1-1),a_2,…a_2,(a_1+1) \right \}$$ $$[a_1,a_2,…a_2,a_1]=\left \{ (a_1-1),a_2,…a_2,(a_1+1) \right \}$$](https://dxdy-03.korotkov.co.uk/f/e/f/6/ef6429592d5a296c8af241659834d80b82.png) И более общее выражение, хотя не завершенное:
И более общее выражение, хотя не завершенное:![$$b[a_1,a_2,…a_2,a_1]=\left \{(a_1-1),a_2,…a_2,a_1,(b-1),1\right \}$$ $$b[a_1,a_2,…a_2,a_1]=\left \{(a_1-1),a_2,…a_2,a_1,(b-1),1\right \}$$](https://dxdy-04.korotkov.co.uk/f/3/a/9/3a909d982f7f7d811f1c3d867f9727d982.png)
Вернемся чуть назад. Последняя пара подх. дробей палиндрома из n знаков имеет вид

(положим A>B>C). Обратная дробь (с добавленным нулем) из (n+1) знаков имеет вид

, причем

Подставим ее в (14) вместо

, делая замены

:

Добавляя ноль справа от палиндрома, получаем последнюю пару

Аналогичные подстановки ведут к

Вывод: чисто приодическая дробь с периодом (0, палиндром) или (палиндром,0) есть квадратный корень из некоторого рационального числа. Верно ли обратное?

– не любые числа, но требованием взаимной простоты не связанные. Единственное ограничение – существование целого

, из чего видно, что
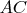
в общем случае не является целым квадратом. Пусть

,

при вз. простых

. Обратное утверждение верно, если для произвольной несократимой дроби

, не являющейся квадратом рациональгого числа, находятся

и

такие, что

, или

Это приводит к известному разрешимому уравнению

. То же и для обратной дроби

Таким образом, каждый квадратный радикал есть чисто периодическая дробь. Период – палиндром с нулем слева или справа в зависимости от того

или

подкоренное значение. Из формул (11), (12) видим, что в окрестности каждой рациональной точки

расположены радикалы

и

с соответствующим полупериодом. Процесс разложения квадратного радикала также можно cвести к полупериоду, если не важны значения старших подх. дробей кроме последних, которые следуют из формул (11), (12). Для решения уравнения

, к примеру, достаточно семи знаков разложения


Алгоритм разложения не фиксирует нулей, отсюда и термин «промежуточная дробь». Из процедуры вместо

получаем приведенную запись

которая, не являясь формально чистым периодом, усложняет выкладки и вызывает вопросы, хотя присутствие удвоенного первого знака в конце периода также следует из вышесказанного. Корень из целого числа выделяется из общего случая тоько тем, что

Тут возникает любопытный вопрос: для всякого ли палиндрома

разрешимо уравнение в целых числах

Или в виде задачи: всякий ли палиндром может быть приближением дробной части целого радикала с точностью до периода?
Две последние подх. дроби палиндрома имеют вид

, причем

Разложению дробной части соответствуют обратные дроби

Прибавим к ним целую часть

Тогда тройка дробей перед нулем принимает вид

В случае целого радикала числитель последней дроби должен делиться на знаменатель предпоследней:

Остается выяснить, при каких условиях последняя дробь оказывается сократимой. Из

и взаимной простоты
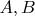
получаем ключевое выражение

которое нужно рассмотреть поподробнее. Если

– нечетные,

вынужденно четное, и такое сравнение неразрешимо. Дробь

, к примеру, не может быть приближением дробной части целого радикала т.к. оба знаменателя последней пары

– нечетные. Если же одно из чисел

– четное, то

Где

– количество знаков палиндрома.
Пример:

Отсюда


… и т.д. Произведение соседних членов последовательности
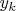
– число вида

или

Рекуррентное правило:

или

в зависимости от четности

Подобные «арифметические прогрессии» из радикалов несовершенны: разность прогрессии, не является целым числом, но стремится к целому числу.
Радикалы степени k
Разложение
![$\sqrt[3]{3}=1,2,3,1,4,1,5,1,1,6,…$ $\sqrt[3]{3}=1,2,3,1,4,1,5,1,1,6,…$](https://dxdy-04.korotkov.co.uk/f/f/2/a/f2a63ddaede58a862208c5ade9fbeaa282.png)
можно легко посчитать на калькуляторе с функцией

, вычитая последовательно целую часть, – процесс, ограниченный точностью вычислительного устройства. Понятно, что раскладывается при этом не сама иррациональность, а десятичное ее приближение, и, поскольку о структуре непериодических последовательностей разложения алгебраических чисел степени

сказать попросту нечего, попробую предложить хотя бы некий гибридный метод разложения радикалов степени

. Определим для начала формулу

-го остатка разложения вещественного

в общем виде. Непосредственно из

следует

- формула, позволяющая получить вышеупомянутым способом дробь, начиная с

-го знака, или хотя бы один ее знак:

Чтобы извлечь лучшее приближение из

Архимеду достаточно было бы подставить в (15) значения:

и получить

, но
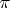
для этого нужно знать с хорошей точностью. Пригодились бы тут его многоугольники - трудно сказать. Сдвиг с мертвой точки в подобных задачах происходит, если удается избавиться от иррациональности в знаменателе. В случае

это не сложно:


Казалось бы противоречие сохраняется: для разложения

требуется знать величину

Но чтобы получить один знак

достаточно целой части

, а значит целой части

, после чего вычисляются элементы дроби

и далее по кругу. Сколько можно получить знаков из разложения (16), если брать

с точностью, имеющейся к моменту

, то есть

– вопрос отдельный. В любом случае такое выражение может быть основой некоторого алгоритма разложения квадратного радикала. Обозначим знаменатель

и рациональную часть числителя

Значение

определено как разность величин, на порядок превосходящих результат, а это могут быть большие числа. При заявленном подходе такие вычисления приходится выполнять на каждом этапе, что есть существенный недостаток в сравнении с классической процедурой, где

появляется естественным образом как знаменатель новой дроби после сокращения. Найти рекуррентную зависимость для членов последовательности

– вполне себе технологический вопрос, который при

оказывается чуть ли не самым интересным. Модифицированный алгоритм для

уже выкладывался здесь:
http://dxdy.ru/topic97794.htmlПодставим теперь в (15) радикал степени

:
![$$a_{n+1}=\left \lfloor -\dfrac{p_{n-1}-\sqrt[k]{m}q_{n-1}}{p_n-\sqrt[k]{m}q_n} \right \rfloor$$ $$a_{n+1}=\left \lfloor -\dfrac{p_{n-1}-\sqrt[k]{m}q_{n-1}}{p_n-\sqrt[k]{m}q_n} \right \rfloor$$](https://dxdy-01.korotkov.co.uk/f/8/6/b/86bffa5f0e34b1de15a9d0bded03a3fd82.png)
и попробуем провести аналогичные преобразования:
![$$-\dfrac{p_{n-1}-\sqrt[k]{m}q_{n-1}}{p_n-\sqrt[k]{m}q_n}=$$ $$-\dfrac{p_{n-1}-\sqrt[k]{m}q_{n-1}}{p_n-\sqrt[k]{m}q_n}=$$](https://dxdy-02.korotkov.co.uk/f/5/f/e/5fe552d4f5faaa0066054de0ddb5e93e82.png)


В левых скобках числителя - (

), в правых – (

) слагаемых, приблизительно равных

, что следует из
![$\sqrt[k]{m}\approx \dfrac{p_n}{q_n}.$ $\sqrt[k]{m}\approx \dfrac{p_n}{q_n}.$](https://dxdy-01.korotkov.co.uk/f/8/c/9/8c9a109758ee9c2d5e3c0163e5b276f582.png)
Обозначим сумму в скобках

, слагаемые в порядке следования -

, и заметим, что произведение пар симметрично расположенных слагаемых

Запишем


. . . . . . . . . . . . . . . .

В полусумме имеем

Рассмотрим один из квадратов правой части.

То же и для остальных. Можно предположить, что с ростом

сумма квадратов стремится к нулю, то есть

Если это верно, то погрешность числителя в итоговой формуле

бесконечно мала. В пользу этого предположения говорит и тот факт, что подстановка

возвращает точное выражение (16). Формула хорошо подтверждается практикой, однако «стартовая» пара подх. дробей должна быть достаточно точной. Иначе получаем 0 или -1 на следующем этапе вычислений (цепные дроби – не та область, где можно пропустить ошибку). Сколько знаков можно получить из разложения (17) помимо одного, и с какой точностью брать при этом квадратный радикал в числителе – вопрос совсем уже отдельный. Вроде бы такой параметр должен расти, и возникает мысль об аппроксимации квадратичными иррациональностями, но тут заходим слишком далеко. В параллельной теме описан
обобщенный алгоритм разложения вещественного корня полинома k-ой степени. Он "менее точен", но точность в данном случае не достоинство, поскольку добавить лишнюю подх. дробь на старте процесса не составляет труда.
По поводу рекуррентного правила последовательности

вопрос когда-то уже выкладывался в иной формулировке. Последовательность

, являясь функцией от последовательности
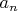
, задается двумя начальными членами

и рекуррентным правилом:

Последовательность
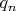
отличается начальными членами:

. Если существует рекуррентное правило для последовательности

, где коэффициенты при членах последовательности – также функция от
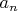
, то оно верно и для

, и для

Задачу возведения в k-ую степень удается свести к линейной системе из k-1 уравнений, но уже при k=2 решение выглядит витиевато:

Перепишем это так:

А лучше так:

![$$\frac{z_{n+1}}{[a_{n+1}][a_n,a_{n+1}]}-\frac{z_n}{[a_n]}-\frac{z_{n-1}}{[a_{n+1}]}+\frac{z_{n-2}}{[a_n][a_n,a_{n+1}]}=0$$ $$\frac{z_{n+1}}{[a_{n+1}][a_n,a_{n+1}]}-\frac{z_n}{[a_n]}-\frac{z_{n-1}}{[a_{n+1}]}+\frac{z_{n-2}}{[a_n][a_n,a_{n+1}]}=0$$](https://dxdy-04.korotkov.co.uk/f/3/3/7/3372f58fc1a5cef5867329677ceb8f2582.png)

![$$\frac{z_{n+1}}{[a_{n+1}][a_n,a_{n+1}][a_{n-1},a_n,a_{n+1}]}-\frac{z_n}{[a_n][a_{n-1},a_n ]}-\frac{z_{n-1}}{[a_{n-1}][a_{n+1}]}+\frac{z_{n-2}}{[a_n][a_n,a_{n+1}]}+\frac{z_{n-3}}{[a_{n-1} ][a_{n-1},a_n][a_{n-1},a_n,a_{n+1}]}=0$$ $$\frac{z_{n+1}}{[a_{n+1}][a_n,a_{n+1}][a_{n-1},a_n,a_{n+1}]}-\frac{z_n}{[a_n][a_{n-1},a_n ]}-\frac{z_{n-1}}{[a_{n-1}][a_{n+1}]}+\frac{z_{n-2}}{[a_n][a_n,a_{n+1}]}+\frac{z_{n-3}}{[a_{n-1} ][a_{n-1},a_n][a_{n-1},a_n,a_{n+1}]}=0$$](https://dxdy-01.korotkov.co.uk/f/0/5/7/05771b6960b55396b44fe01556ffb03f82.png)

, не влезая в строку, выглядит аналогично, но «и т.д.» ставить рановато. Увидеть закономерность удается только с помощью матрицы (8), расставляя континуанты знаменателей по своим местам (как в пазлах):
Вложение:
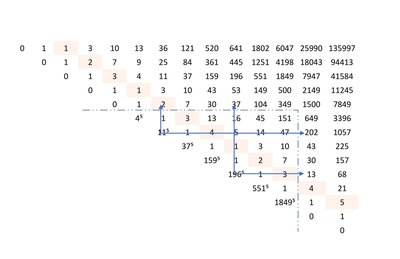 M2.jpg [ 76.89 Кб | Просмотров: 0 ]
M2.jpg [ 76.89 Кб | Просмотров: 0 ]
Положим k=5. Выберем 7 (k+2) элементов третьей строки, спроецируем их на нулевую диагональ, впишем вместо нулей соответствующие степени и очертим подматрицу с большой диагональю из выбранных степеней в качестве основания. Тогда произведение элементов подматрицы, «покрываемых» лучами, исходящими из каждой степени – и есть соответствующий ей знаменатель знакопеременного выражения. То есть


Повторюсь, элементы строки и сама строка выбирались произвольно. В основании подматрицы могли быть степени элементов другой строки, суммы степеней элементов общего столбца из разных строк или многочлен с постоянными коэффициентами при k-ых степенях, в том числе и

(если
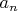
– разложение радикала k-ой степени). Тут интерес уже не в

, а в неком универсальном свойстве матрицы (8), о применимости которого остается догадываться, хотя преодолеть подслеповатость Excel’я при разложении
![$\sqrt[11]{m}$ $\sqrt[11]{m}$](https://dxdy-03.korotkov.co.uk/f/6/4/a/64a069295528d8227b905056af925f1b82.png)
таким способом удается прекрасно. Гипотеза проверена в общем виде для k=5. Похоже на индукцию, где вместо логического перехода k - (k+1) употреблена умозрительная экстраполяция свойства матрицы (8) на (k+1)-ый уровень. Решение?



