Продолжаю прорешивать задачи из книжки Давидовича и ко
http://www.mccme.ru/free-books/57/davidovich.pdf.
В этой теме - листок 13.
Прошу уважаемых форумчан проверить мои доказательства, как и в моих предыдущих темах. Помимо всего прочего, буду благодарен за замечания по стилистике доказательств.
Определение 1.
Точка

(все множества, встречающиеся в данном листке, предполагаются подмножествами

) называется внутренней точкой множества

, если существует окрестность точки

, целиком лежащая в

.
Определение 2.
Множество называется открытым, если все его точки внутренние.
Задача 1.
Пересечение конечного числа открытых множеств открыто.
Доказательство.
Возьмем произвольную точку

из пересечения конечного числа открытых множеств. Каждое множество из пересечения содержит некоторую окрестность точки

. Значит, их пересечение должно содержать наименьшую из окрестностей. Следовательно, пересечение также является открытым множеством.
-- 12.07.2017, 12:03 --Задача 2.
Объединение любого числа открытых множеств открыто.
Доказательство.
Возьмем произвольную точку

из объединения открытых множеств.

вместе с некоторой своей окрестностью принадлежит какому-то множеству из объединения. Значит эта же окрестность точки

принадлежит объединению. Следовательно, объединение также является открытым множеством.
-- 12.07.2017, 12:03 --Задача 3.
Всегда ли пересечение счетного числа открытых множеств открыто?
Ответ.
Нет, не всегда. Например, существуют системы вложенных интервалов, чье пересечение состоит из одной точки (см. задачу 17 листка 8).
-- 12.07.2017, 12:04 --Задача 4*.
Всякое открытое множество есть либо прямая, либо объединение не более чем счетного числа попарно непересекающихся интервалов и открытых лучей.
Вот эту задачу пока пропускаю, требует обдумывания.
-- 12.07.2017, 12:05 --Определение 3.
Точка

называется предельной точкой множества

, если любая окрестность точки

содержит хотя бы одну точку множества

, отличную от

. Множество предельных точек множества

обозначается

.
Задача 5.
Всегда ли предельная точка последовательности
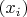
является предельной точкой множества

?
Ответ.
Нет, не всегда. Например, если предельная точка

последовательности
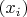
является таковой из-за равенства ей бесконечного числа членов
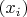
(пример: последовательность

с предельной точкой

); в таком случае могут существовать окрестности

, не содержащие ни одной точки множества

.
-- 12.07.2017, 12:06 --Определение 4.
Точка

называется предельной точкой множества

, если существует сходящаяся к

последовательность точек
множества

.
Задача 6. Определения 3 и 4 равносильны.
Доказательство.
Пусть

-- предельная точка множества

по определению 3.
Алгоритм формирования из точек

последовательности, сходящейся к точке

, следующий. Возьмем произвольную окрестность точки

и возьмем из нее точку

, отличную от

. Далее, на каждом (

-м) шаге сужаем взятую на предыдущем шаге окрестность и берем из новой окрестности точку

, отличную от

. В итоге получим последовательность

из точек

, сходящуюся к точке

, т.е. выполнено определение 4.
Пусть теперь

-- предельная точка множества

по определению 4, и пусть
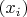
-- последовательность из точек

, сходящаяся к точке

.
Сходимость
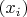
к

означает, что в любой окрестности точки

содержатся почти все члены
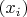
, т.е. бесконечно много точек

. Очевидно, из этого следует что любая окрестность точки

содержит хотя бы одну точку множества

, т.е. выполнено определение 3.
-- 12.07.2017, 12:07 --Определение 5.
Точка

называется изолированной точкой множества

, если существует окрестность точки

, не содержащая других точек множества

.
Задача 7. Всякая точка множества

является или предельной, или изолированной точкой

.
Доказательство.
Пусть

-- произвольная точка произвольного множества

.
Возьмем произвольную окрестность точки

. Если она не содержит ни одной точки множества

, то

является изолированной точкой. Если содержит хотя бы одну точку, то сужаем окрестность например в 2 раза, и смотрим на содержание точек в новой окрестности. Повторяем процесс. Если наткнулись на окрестность без точек, значит

изолирована, если каждая окрестность содержит точки, то предельная (по определению 3).
-- 12.07.2017, 12:08 --Задача 8.
Если ограниченное множество

бесконечно, то

непусто.
Доказательство.
Если

несчетно, то из него можно выделить счетное подмножество (задача 13 листка 4); если счетно, то берем само

.
Элементы счетного подмножества множества

можно представить в виде последовательности, причем без повторяющихся членов. Эта последовательность ограничена. Из ограниченной последовательности можно выделить как минимум одну сходящуюся последовательность (задача 16.а листка 11), причем ее предел

будет являться также пределом последовательности из тех же членов за вычетом самого

(это следует из уникальности членов), а значит и предельной точкой множества

(по определению 4).



