Пусть взаимно-простые целые положительные числа

,

и

удовлетворяют уравнению Ферма:

, где

- простое число, большее двух.
Существуют простые способы доказательства первого случая ВТФ: невозможность равенства Ферма, если

не делится на

.
В частности, можно применить теорему Лежандра, основанную на методе Софи Жермайн: если

не делится на

, и

- простое число, или

- простое число, то равенство Ферма невозможно.
Доказательство теоремы Лежандра находится в книге "Fermat Theorem For Amateurs", на стр. 112.
Для доказательства первого случая ВТФ, можно также использовать детерминант Вендта, но наиболее универсальный критерий даёт теорема Фуртвенглера, которая имеет простое доказательство (смотрите мою тему "Теорема Фультвенгера").
Из теоремы Фуртвенглера следует невозможность равенства Ферма в первом случае ВТФ, если

.
Из изложенного ясно, что для

, если

не делится на

, то равенство Ферма

невозможно.
В этой теме мы изложим новый общий метод доказательства второго случая ВТФ и применим его для

.
Пусть

делится на

.
Из равенства

следует:

, где

.
Из условия

делится на

следует, что

не делится на

.
Покажем, что в кольце целых алгебраических чисел поля
![$\mathh{Q}[\sqrt[n]{2}]$ $\mathh{Q}[\sqrt[n]{2}]$](https://dxdy-01.korotkov.co.uk/f/0/2/5/02578322f6f0f3a1810a0ffb3358d34c82.png)
, для

, число
![$z^2-x y \sqrt[n]{2}$ $z^2-x y \sqrt[n]{2}$](https://dxdy-03.korotkov.co.uk/f/a/6/4/a64b86d10dd00c1a395884e8c567449282.png)
является квадратом.
Лемма 1
-----------
Обозначим
![$g=\sqrt[n]{2}$ $g=\sqrt[n]{2}$](https://dxdy-01.korotkov.co.uk/f/4/1/3/4133b94ec39cc4ee7147cfe2693b71a382.png)
.
Пусть

и
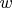
- целые взаимно-простые числа, и

делится на

.
Пусть

.
Если

- нечётное число, то числа

и

не имеют в кольце
![$\mathbb{Z}[g]$ $\mathbb{Z}[g]$](https://dxdy-04.korotkov.co.uk/f/b/f/e/bfec15f8b72d734ed990479e44472c4c82.png)
общих делителей - идеалов.
Если

- чётное число, то числа
![$(u-v)/\sqrt[n]{4}$ $(u-v)/\sqrt[n]{4}$](https://dxdy-01.korotkov.co.uk/f/4/e/f/4ef7957e5456d7c4e4f8ac7bf104f68282.png)
и
![$(u^{n-1}+v u^{n-2}+...+v^{n-2} u+v^{n-1})/(\sqrt[n]{4})^{n-1}$ $(u^{n-1}+v u^{n-2}+...+v^{n-2} u+v^{n-1})/(\sqrt[n]{4})^{n-1}$](https://dxdy-04.korotkov.co.uk/f/b/e/2/be2f427bdf98740312268f931b31169282.png)
не имеют в кольце
![$\mathbb{Z}[g]$ $\mathbb{Z}[g]$](https://dxdy-04.korotkov.co.uk/f/b/f/e/bfec15f8b72d734ed990479e44472c4c82.png)
общих делителей - идеалов.
Доказательство
--------------------
Деля полином

на полином

получим остаток

.
Значит число

делится на любой общий делитель чисел

и

.
Число

взаимно-просто с числом

, в силу того, что одно из чисел

и

делится на

, а второе - взаимно-просто с

.
Число
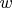
тоже взаимно-просто с числом

, поскольку взаимно-просто с числом

.
Значит число
![$(\sqrt[n]{4})^{n-1}$ $(\sqrt[n]{4})^{n-1}$](https://dxdy-01.korotkov.co.uk/f/8/e/7/8e71e8ff02428a72ba4bbb82ae29d40b82.png)
делится на любой общий делитель чисел

и

.
Если

- нечётное число, то числа ִִ
![$\sqrt[n]{4}$ $\sqrt[n]{4}$](https://dxdy-03.korotkov.co.uk/f/2/4/9/249b088fd9588ff7ad83532aba75926c82.png)
и

взаимно-просты, следовательно числа

и

не имеют общих делителей.
Если

- чётное число, то числа ִִ
![$\sqrt[n]{4}$ $\sqrt[n]{4}$](https://dxdy-03.korotkov.co.uk/f/2/4/9/249b088fd9588ff7ad83532aba75926c82.png)
и
![$(u-v)/\sqrt[n]{4}$ $(u-v)/\sqrt[n]{4}$](https://dxdy-01.korotkov.co.uk/f/4/e/f/4ef7957e5456d7c4e4f8ac7bf104f68282.png)
взаимно-просты, следовательно числа
![$(u-v)/\sqrt[n]{4}$ $(u-v)/\sqrt[n]{4}$](https://dxdy-01.korotkov.co.uk/f/4/e/f/4ef7957e5456d7c4e4f8ac7bf104f68282.png)
и
![$(u^{n-1}+v u^{n-2}+...+v^{n-2} u+v^{n-1})/(\sqrt[n]{4})^{n-1}$ $(u^{n-1}+v u^{n-2}+...+v^{n-2} u+v^{n-1})/(\sqrt[n]{4})^{n-1}$](https://dxdy-04.korotkov.co.uk/f/b/e/2/be2f427bdf98740312268f931b31169282.png)
не имеют общих делителей.
Лемма 2
-----------
Пусть

- числовое поле cо степенью

расширения

, где

- сигнатура

.
Пусть

, где

- дискриминант поля

.
(A) Пусть любое простое число, которое не больше чем

, разлагается в произведение простых главных идеалов.
Тогда любой идеал

поля

является главным.
Доказательство
---------------------
Cогласно (ссылке I), существует такое число

, принадлежащее идеалу

, что:
(1)

Следовательно

.
Следовательно идеал

является делителем целого положительного числа, не превосходящего

.
Такие делители являются главными идеалами, в силу условия (A).
Следовательно

является главным идеалом.
Что и требовалось.
Лемма 3
-----------
Для

: поле
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
является полем главных идеалов.
Доказательство
--------------------
Для

:

соответственно, где

- число определённое в лемме 2.
Следующий код на языке математической программы "Sage" проверяет, что условие (A) леммы 2 выполняется:
Код:
n=5;
K.<a>=NumberField(x^n-2);K
P=[3, 5, 7, 11, 13];
for m in P:
I=K.ideal(m);
F=I.factor();
for J in F:
print(m, J[0].gens_reduced(), J[0].is_principal())
n=7;
K.<a>=NumberField(x^n-2);K
P=[3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89];
for m in P:
I=K.ideal(m);
F=I.factor();
for J in F:
print(m, J[0].gens_reduced(), J[0].is_principal())
Продолжение следует.



