I downloaded interesting book for a systems and thought about finding a common method for solving similar systems in a pure algebraic way (without using conics). I found something that works for all the similar systems in the book. Take the coefficients before

,

,

. Let them be

,

,

- they are fixed numbers. Then try to find a representation of the form
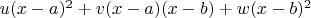
. After expanding the brackets a system of first degree can be formed for

and

using the coefficients before

and

. I'm wondering for what kind of similar systems it works. Probably not for all possible. I suppose it works when a "linear combination" of the initial equations can be factorized or the centers of the two conics are the same.