Спасибо за замечание, но начало этой темы устарело.
.
Оказалось, что закон квадратичной взаимности решает проблему с делителями единицы поля
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
для доказательства ВТФ с использованием этого поля.
Пусть
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
- кольцо целых алгебраических чисел поля
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
.
Почти всегда
![$A(\sqrt[n]{2})=\mathbb{Z}[\sqrt[n]{2}]$ $A(\sqrt[n]{2})=\mathbb{Z}[\sqrt[n]{2}]$](https://dxdy-03.korotkov.co.uk/f/a/c/8/ac80b8daf92b4fc31348a20599e96be782.png)
, но для некоторых

может отличаться от этого кольца.
Для того, чтобы доказать ВТФ, используя кольцо
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
нужно сделать 3 вещи:
1) Доказать что в этом кольце все идеалы - главные.
2) Доказать, что любой положительный делитель единицы этого кольца с чётными коэффициентами при нечётных степенях
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
является квадратом в этом кольце.
3) Доказать, что равенство
![$x^2-yz (\sqrt[n]{2})^2=\alpha^2$ $x^2-yz (\sqrt[n]{2})^2=\alpha^2$](https://dxdy-04.korotkov.co.uk/f/b/2/6/b26477ae3d188428ef46d3c17c6f5ef082.png)
невозможно, где
![$\alpha \in A(\sqrt[n]{2})$ $\alpha \in A(\sqrt[n]{2})$](https://dxdy-03.korotkov.co.uk/f/a/4/7/a4792ddcefa693fcdb7020e63805470482.png)
.
Оказывается, можно не доказывать пункт 2) исходя из следующих соображений.
Пусть
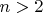
- простое число и

- ненулевые, взаимно-простые целые числа, которые удовлетворяют уравнению Ферма:

.
Пусть

- нечётное число и

не делится на

.
Предположим, все идеалы кольца
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
- главные.
При этих предположениях имеет место равенство:
(1)
![$e_1 (x^2-yz (\sqrt[n]{2})^2)=\alpha^2$ $e_1 (x^2-yz (\sqrt[n]{2})^2)=\alpha^2$](https://dxdy-01.korotkov.co.uk/f/c/c/a/cca7ec27f80be7c5771db8f1bd813b2082.png)
, где

- положительный делитель единицы кольца
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
и
![$\alpha \in A(\sqrt[n]{2})$ $\alpha \in A(\sqrt[n]{2})$](https://dxdy-03.korotkov.co.uk/f/a/4/7/a4792ddcefa693fcdb7020e63805470482.png)
.
Известно, что

делится на

.
Простое доказательство этого находится на стр. 189 книги Риббенбойма "Fermat's Last Theorem For Amateurs".
Я обнаружил в этом коротком доказательстве две опечатки: вместо "By Chapter II, (3A)" должно быть "By Chapter III, (2A)" и вместо "This contradicts Lemma 2.2" должно быть "This contradicts Lemma 2.1".
Из (1) следует:
(2)

по модулю

, поскольку

делится на

.
В начале 20-го века Гекке доказал закон квадратичной взаимности для любого числового поля.
Доказательство этого закона находится в книге Гекке "Лекции по теории алгебраических чисел".
Закон сформулирован на стр. 244 (теорема 165).
Пусть

- кольцо целых алгебраических чисел некоторого числового поля.
Число

называется примарным, если оно сравнимо с квадратом числа кольца

по модулю

.
Число

называется нечётным, если оно взаимно-просто с числом

, то есть если

для некоторых

.
В кольце
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
нечётные числа это числа не делящиеся на
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
.
Для кольца
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
, закон квадратичной взаимности Гекке имеет особенно простой вид:
(3)

,
где

и

-любые нечётные взаимно-простые числа, принадлежащие кольцу
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
, из которых хотя бы одно примарное.
Из (2) и (3) следует:
(4)

, для любого нечётного числа
![$b \in A(\sqrt[n]{2})$ $b \in A(\sqrt[n]{2})$](https://dxdy-01.korotkov.co.uk/f/4/f/0/4f02c4ccbc7e7eac4e56196d93faa54c82.png)
,
где

и

- квадратичные символы (а не дроби).
Из (4) следует:
(5)

, для любого нечётного числа
![$b \in A(\sqrt[n]{2})$ $b \in A(\sqrt[n]{2})$](https://dxdy-01.korotkov.co.uk/f/4/f/0/4f02c4ccbc7e7eac4e56196d93faa54c82.png)
.
поскольку

по определению квадратичного символа для делителя единицы

.
Из (5) следует:
(6) число

является квадратом в кольце
![$A(\sqrt[n]{2})$ $A(\sqrt[n]{2})$](https://dxdy-02.korotkov.co.uk/f/9/e/6/9e60f049ed02d3e31766b756ad5f63c082.png)
,
в силу теоремы 65:15 на стр. 182 книги O'Meara "Introduction to quadratic forms".
Эта теорема называется "Global Square Theorem" и является частным случаем локально-глобального принципа Хассе.
Из (1) и (6) следует:
(7)
![$(x^2-yz (\sqrt[n]{2})^2)=\alpha^2$ $(x^2-yz (\sqrt[n]{2})^2)=\alpha^2$](https://dxdy-04.korotkov.co.uk/f/f/1/1/f11e2cfb6755592495a3c7515a119d1a82.png)
, где
![$\alpha \in A(\sqrt[n]{2})$ $\alpha \in A(\sqrt[n]{2})$](https://dxdy-03.korotkov.co.uk/f/a/4/7/a4792ddcefa693fcdb7020e63805470482.png)
.
Равенство (7) позволяет перейти к пункту 3) не доказывая пункт 2).
Я считаю это доказательство своим вторым достижением на форуме после доказательства ВТФ для
.
Хотелось бы, чтобы его проверили.