Вот сравнительно простое доказательство. Вместо

я буду использовать обозначение

.
Далее через

будем обозначать произвольное решение системы с начальными данными

. В частности

. Это слегка упростит начертание формул.
Выберем произвольное

и зафиксируем его. Для всех

индуктивно определим

следующим образом

А далее в силу условия устойчивости решения

полагаем

и если

, то

для всех

.
Положим

. А через

обозначим образ этого множества под действием системы (ставим задачу Коши с данными из

и решаем на интервале
![$[0,t]$ $[0,t]$](https://dxdy-02.korotkov.co.uk/f/9/9/0/990afe3dc2a01ee124e9c8ef79e63b2182.png)
). Отмечу, что по условию, меры всех этих множеств одинаковы и равны некой величине
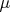
. Объединение всех этих множеств -

. Выберем конечное множество точек

так, чтобы

Без потери общности считаем, что среди этих

есть и
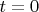
. Если нет - добавим.
Наконец положим

таким образом, что

. Я утверждаю, что на любом интервале вида

найдется квазипериод функции

, согласованный с

Ну действительно, по построению

для некоторого

. Ибо не покрытое множество имеет малую меру. Это значит, что найдется

такое, что

, а значит

. Дальше все стандартно. Обозначим

. По построению

.
Поскольку

, то

Поскольку

, то

В силу выбора

имеем

Складываем и получаем

И, наконец, отсюда следует для всех


Вот вроде и все. Надеюсь, не наврал.